
●
● From tangles to quantum electrodynamics
● From tangles to g-factor diagrams
● The Feynman vertices of the standard model
● Fermion tangles
● Boson tangles
● The electron tangle
● Mathematical challenges with prizes
● Some illustrated tangle challenges with prizes
● The origin of wave functions from tangles
● From strands to quantum field theory
● Literature
Particle physics, including QED, follows from tangled strands.
Tangled strands with Planck radius explain the origin of wave functions and quantum fields, as explained in this text that forms the basis for the following. Tangles explain, for each elementary particle, its origin, its quantum numbers, and its generation. Tangles explain the origin of the three gauge interactions and of their Lie groups. Tangles explain the full Lagrangian of the standard model and thus that of quantum electrodynamics, as shown in the figures below, and also in this publication.
Tangled strands explain the Higgs mechanism, the symmetry breaking of SU(2) and its maximum parity violation. Tangled strands explain the quark model. Tangled strands explain the origin of every Feynman vertex and thus of the Lagrangian of the standard model with massive neutrinos. Tangled strands explain the origin of the fundamental constants: particle masses, including neutrino masses, coupling constants and mixing angles. The numerous experimental predictions and consequences, listed here, agree with every experiment ever conducted.
Because no other approach in the literature provides all these results, it makes sense to calculate the fundamental constants using tangles and their shapes.
The value of each coupling constant is due to the amplitudes for gauge boson emission or absorption. In particular, photons are first Reidemeister moves: photons are twists. Electric charges emit twists. Therefore, electric charge is due to tangle chirality.
The mass value of each elementary particle describes the coupling of rotation and propagation. Therefore, also particle masses are due to tangle chirality. (The Higgs coupling is also reproduced but is left for a later stage of the investigation.)
At least two mathematical ways to quantify the chirality of tangles are thus
needed. This is a general mathematical challenge. This
general challenge yields several specific challenges about knot and tangle
geometry given below. Prizes are offered for their solution.
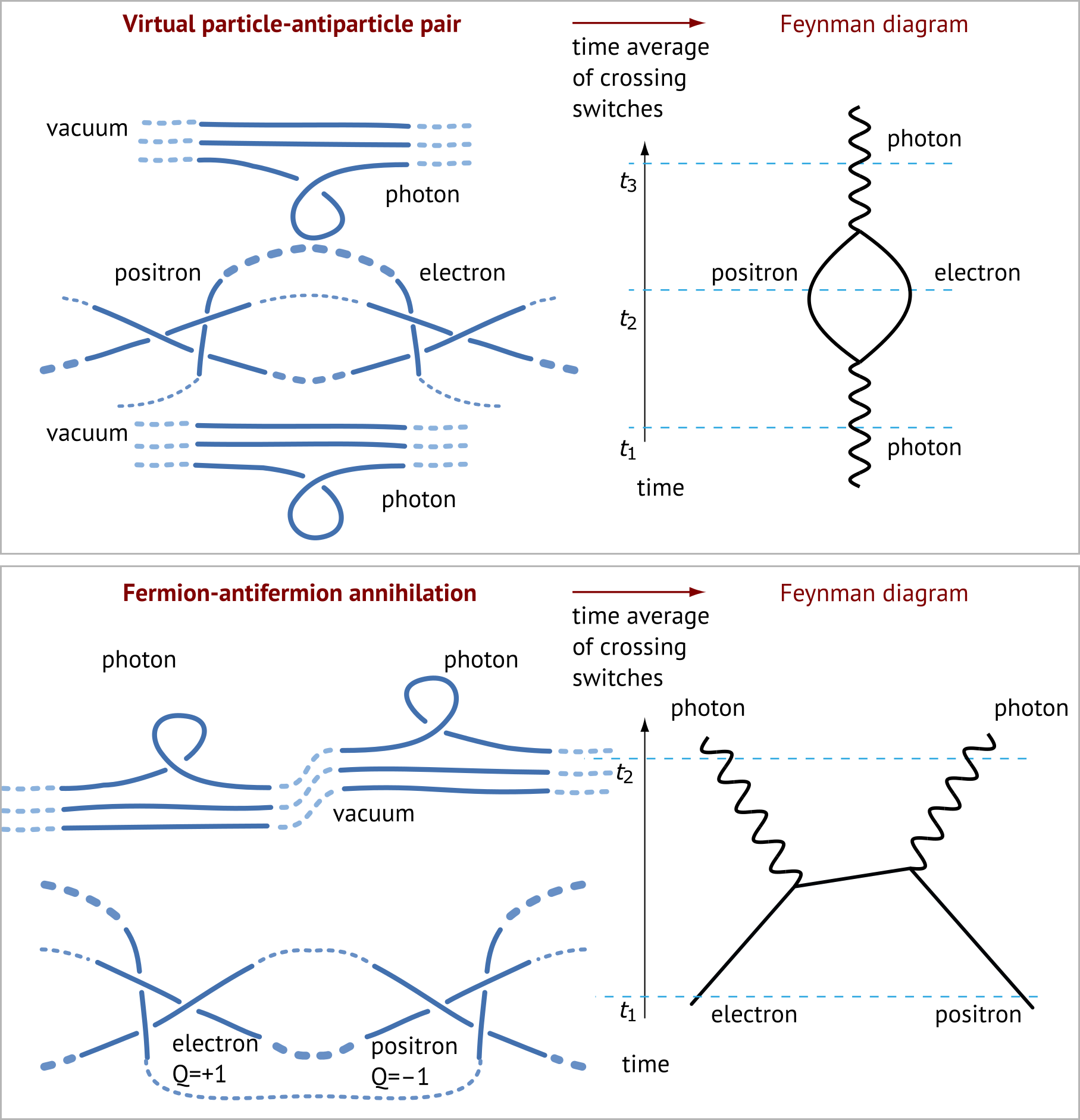
From tangles to quantum electrodynamics
The tangles for the electron and the photon yield the following
dictionary between the strand tangle model and Feynman graphs.

From tangles to g-factor diagrams
The strand tangle model explains, because of Dirac's trick, that the g-factor has the (approximate) value 2. The value 2 assumes rigid rotation of the tangle core. But the strand tangle model also explains why the g-factor slightly deviates from the value 2: in nature, the rotating tangle core does not remain completely rigid. Therefore the g-factor slightly deviates from the value 2.
In the tangle model of elementary particles, not only does charge rotate twice as fast as mass. This was already known for a long time, and is told by Ohanian and by Sebens. In addition, in the tangle model, charge rotation differs slightly from twice the mass rotation. The tangle model explains the difference. Note that no other explanation of this so-called g-factor anomaly is available.
The explanation of the g-factor arises because the tangle model reproduces perturbative QED. As illustrated above, the tangle model reproduces all Feynman vertices. As a consequence, tangles explain Schwinger's first-order expression for the g-factor – a result that has already been published. (Work on the higher orders is ongoing.)
The following pictures show how the tangle model
explains the simplest Feynman diagrams that generate the anomalous magnetic
moment. As mentioned, in these graphs, strands are not observable, only
crossing switches are. As illustrated above, a triangular core
characterizes the electron tangle. Photons are described by a twist, or
loop, in a single strand. The definition of phase given in this
text – and illustrated below – then yields the anomaly.
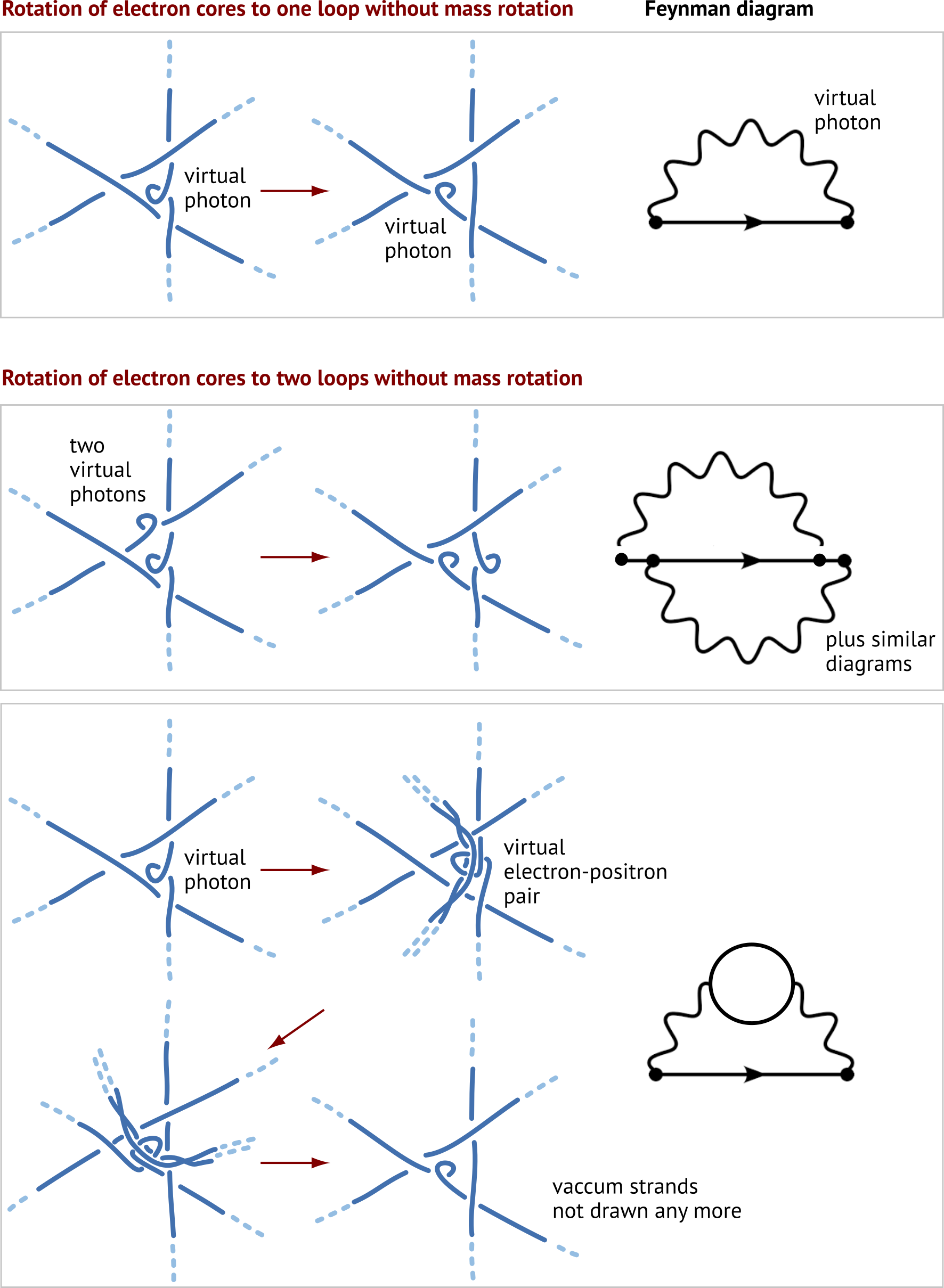
The first row yields Schwinger's expression for the g-factor to the first order in the fine structure constant α. For the g-factor expression to the second order in α, the second row is known to yield the zeta(3) term and part of the rational term. The bottom two rows are expected to lead to the other terms. However, no confirmation exists yet.
The description of electrons with tangles thus suggests an alternative way to compute its g-factor.
The Feynman vertices of the standard model
The fundamental principle of the strand tangle model yields the vertices
of the standard model, without modifications.

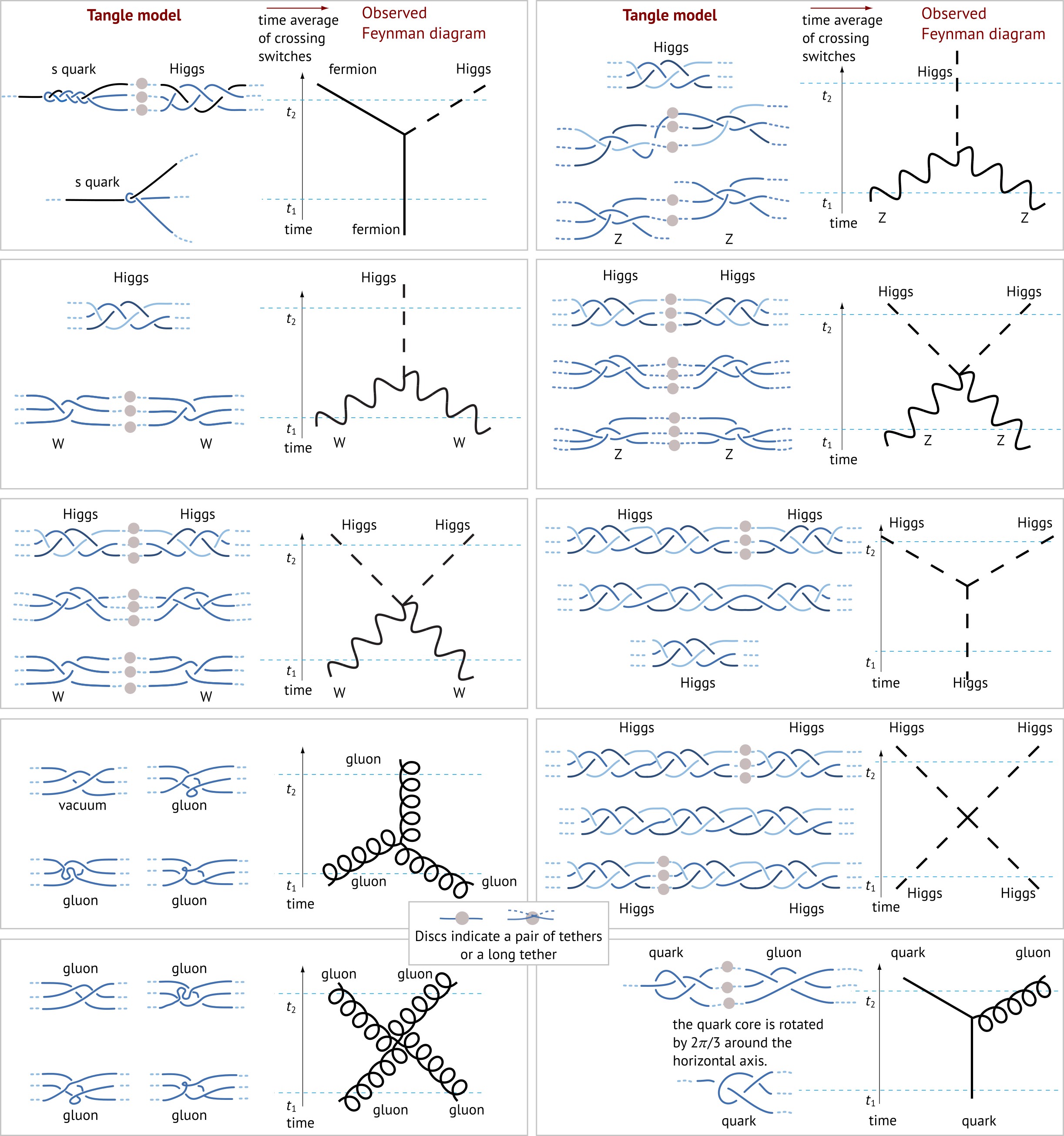
Fermion tangles
Classifying fermion tangles yields the following structures.
(As the fundamental principle states, single, untangled strands are not
observable, only their crossing changes are. Details and publications are provided
here.)

Additional elementary fermions are not possible.
Boson tangles
Classifying boson tangles, helped by the Dirac trick and the
Reidemeister moves, yields the following structures:
Additional elementary bosons are not possible.
The electron tangle
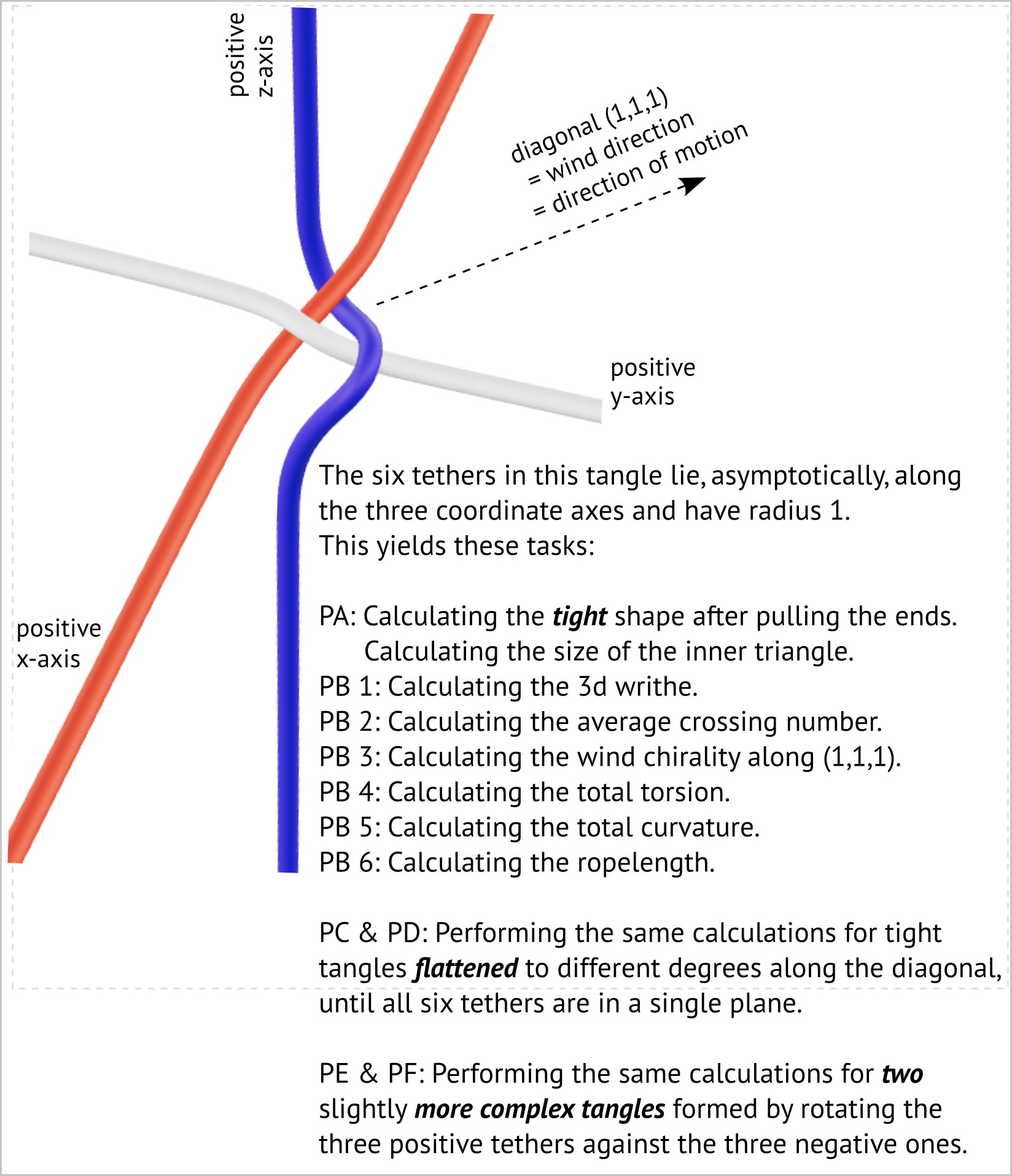
Elementary fermions can only consist of two or three strands. Quarks consist of two strands, leptons of three. The classification of rational tangles – given below – yields exactly the known elementary particles. For an electron at rest, the following tangle arises. All six tethers leave along the coordinate axes. (Knot investigations show that the average shape of a fluctuating tangle is given by the shape of the tight tangle.)
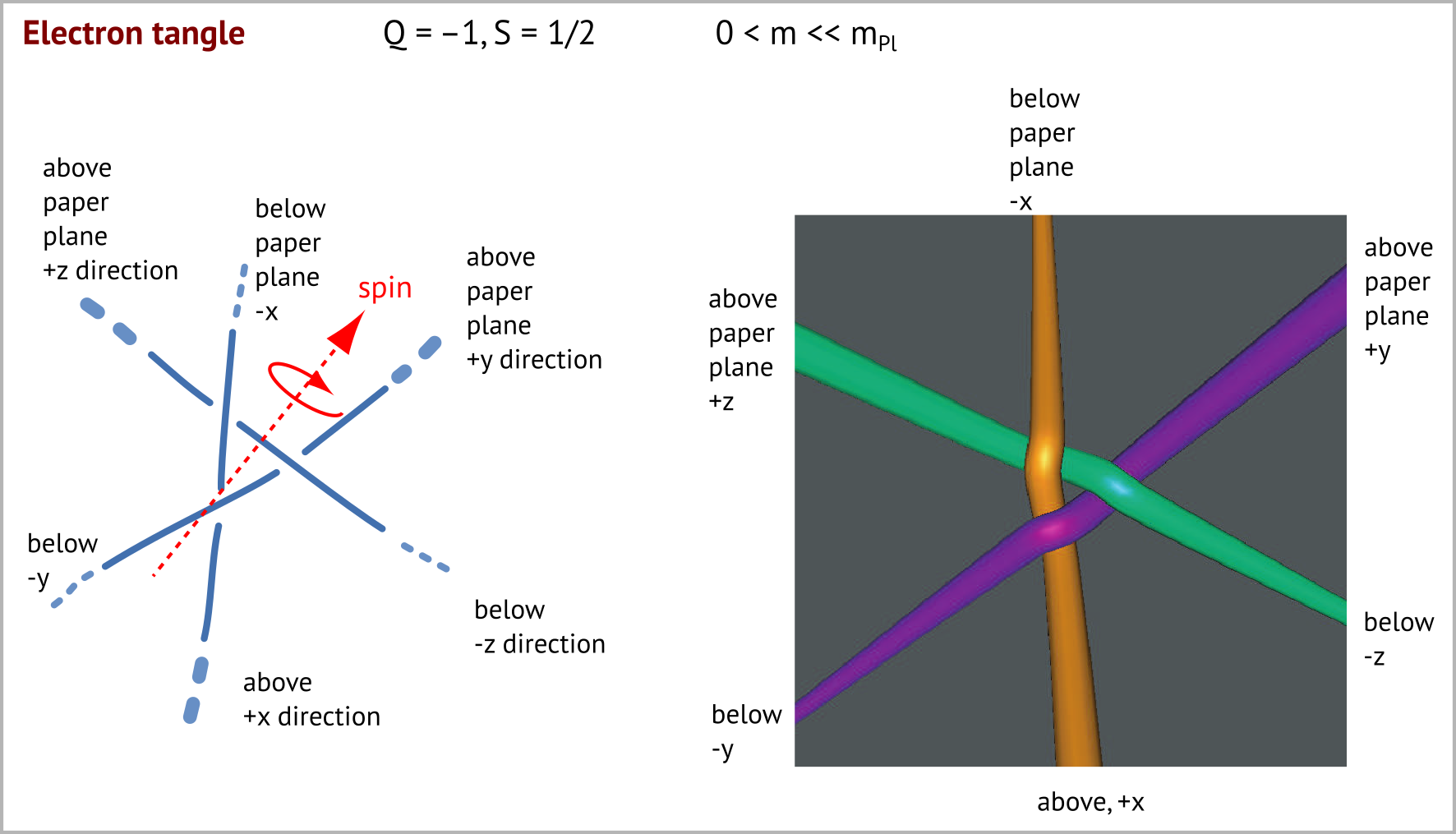
The interactive 3d version of the electron tangle (use the cursor to click and draw):

Note the difference to this tangle, which consists just of three straight strands:

For an electron moving towards the reader, the spinning motion is depicted below, in an animation by Fabrice Neyret (used with permission). The triangle-like structure rotating in the centre is the tangle core of the electron. The rotation axis is marked by a central, green-white circle. This animation assumes rigid core rotation and reproduces the g-factor 2. (It contains some minor geometry errors.) The six tethers leave along the coordinate axes; the observation direction is (1, 1, 1).
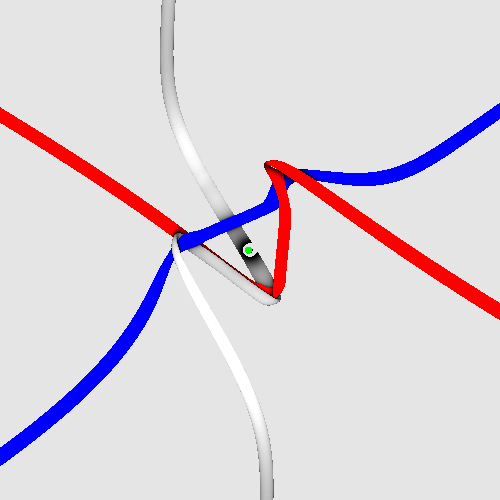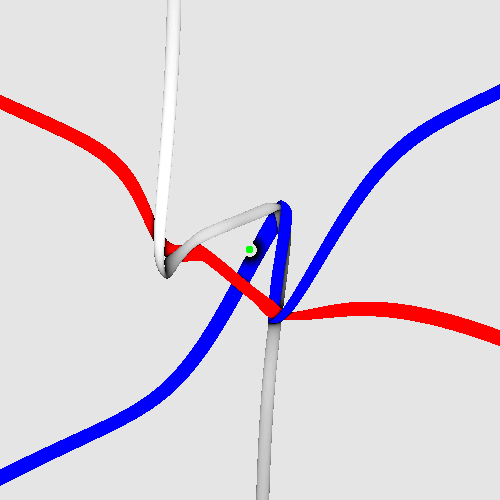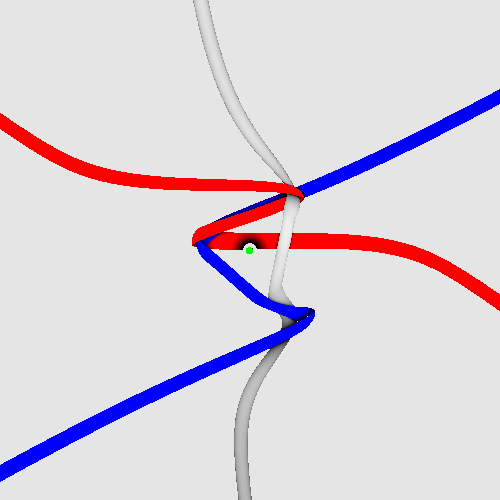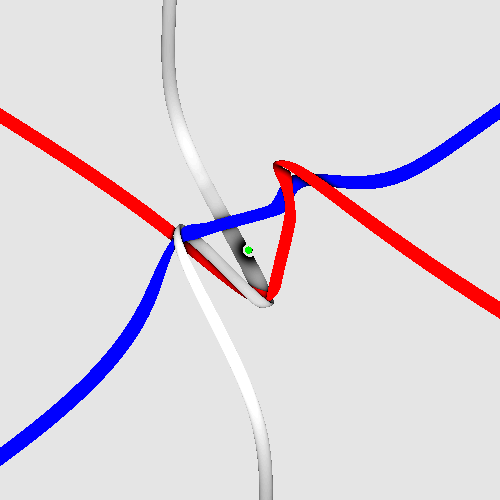
I offer a special prize for producing a tight version of this animation, i.e., based on elastic strands of constant radius that are easy to bend, easy to make longer, but that still tend to be as short as possible. The motion can be imagined to be induced by frictionless wind blowing along (1, 1, 1) hitting the strands. The code is at https://www.shadertoy.com/view/cld3zX.
Mathematical challenges with prizes
Note: do not submit anything if you used AI systems anywhere in or for your submission. Such submissions are not acceptable and not accepted. (There are lies, damned lies, and AI systems. Sapere aude!)
1. The value of the electron mass describes the intensity of the propeller effect of its tangle core. If a fluid flows with speed v perpendicularly through the paper plane of the green-yellow-blue electron tangle shown above, how fast does the tangle with its strands with Planck radius rotate? If you have a suggestion on how to estimate the angular velocity resulting from a speed v, I'd be interested to hear from you at christoph@motionmountain.net. I offer a prize for any good hint and will publish a paper with you.
2. Is the 3d writhe of tight alternating rational tangles with a few crossings quantized and if so, what is the value of the 3d writhe quantum? (For tight alternating knots with a few crossings, the 3d writhe is quantized in multiples of 1/7.) See the pictures below for the precise tangles that are meant. I offer 200 Euro for an answer. (Literature on the writhe of knots is found here.)
3. Is there a good analytical approximation to the shape of the
tight electron tangle with radius 1? (See the figures above and below.) I
offer 200 Euro for an answer. There is no prize for an exact
solution because an exact solution is highly unlikely: you will win almost
every prize that exists in mathematics if you find it. (Not even the
shape of the overhand knot is known exactly.)
3b. What is a good approximation for the size of the inner triangle of the
three tight charged lepton tangles with unit strand radius? I offer 50
Euro for an answer.
4. How can the "wind chirality" – the tensor Q defined in arxiv.org/2004.10338 – be approximated precisely for tight tangles? (Note that wind chirality depends on the direction.) More challenges are listed in the figure below. I offer a prize for each answer.
5. Is there a "twist chirality" that explains the probability of twist emission or absorption? I offer 200 Euro for a good answer. Twist chirality should measure the twistiness of a tangle separately for each direction in space. (If desired, I will provide more details via mail.)
6. Do 3d writhe, wind chirality, or some other measure of chirality change (roughly) logarithmically with the flattening of the tether frame, i.e., with the flattening of the 6 tethers that keep the lepton localized? Several measures of chirality are predicted to show this behaviour. I offer 200 Euro for a positive answer with proof. Less for a negative answer.
7. Does a tight flat electron tangle, with all its tethers in a plane, with a finite central triangle exist? Probably not, as the inner triangle is not limited. Is there only a tight tangle for almost flat tangles? What is the size of the triangle as a function of the squashing of the tangle? What is the shape of the triangle? I offer a prize for each answer.
8. What is the 3d writhe of the flat or almost flat electron tangle? What is its wind chirality? What is its twist chirality? And for the muon and tau tangles? I offer a prize for each answer.
9. Can the rotating tangle core shown above be done with repulsive curves of Keenan Crane and his group? I offer 200 Euro for a visualization.
10. Do you have any proposal for good animations on tangles, such as those described with images on this website? I will give you a prize for it and mention you in publications.
A few additional mathematical prizes, topics for theses, and problems for future publications are found on the prize page. All prizes are for the first solution sent in. (Der Rechtsweg ist ausgeschlossen.)
Some illustrated tangle challenges with prizes
The origin of wave functions from tangles
The fundamental principle of the strand tangle model implies:
Wave functions are blurred tangles.
Wave functions are crossing densities of tangles.
Tangles are skeletons of wave functions.
See this
pedagogical text for the detailed proof.
The relation between tangles and wave functions is given here:
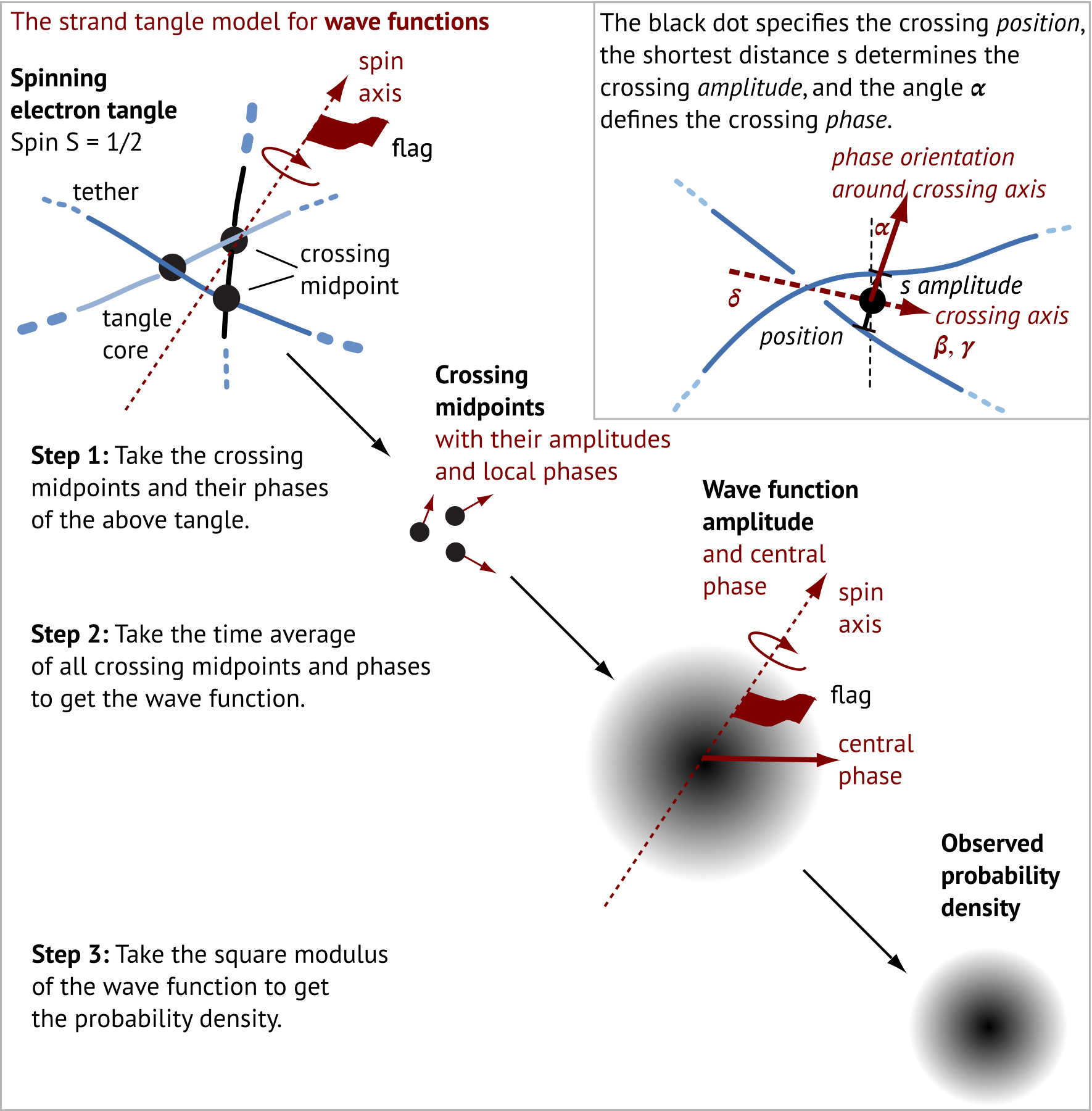
Defining wave functions as blurred tangles yields Hilbert spaces, interference, entanglement, decoherence, and measurements.
From strands to quantum field theory
In the tangle model, strands themselves are not observable. Only switches of crossings are observable. The crossing densities in the tangled region yield spinor wave functions.
Particles are rotating rational 3d tangles of strands. The rational 3d tangles describing particles also describe antiparticles, reactions, interactions and decay.
If one imagines that strands have zero radius and that tangles are pointlike, one gets pure quantum field theory. However, in this case, particle masses and coupling constants cannot be calculated but must be introduced by hand.
For strands of Planck radius, there are deviations at Planck scales. These are unmeasurable. However, particle masses and coupling constants can be calculated.
Literature
T. Aoyama, T. Kinoshita and M. Nio, Theory of the anomalous magnetic moment of the electron, Atoms, 7 (2019) 28.
C. Cerf and A. Stasiak. A topological invariant to predict the three-dimensional writhe of ideal configurations of knots and links. Proceedings of the National Academy of Sciences, 97 (2000) 3795–3798.
P. Hoidn, R.B. Kusner and A. Stasiak, Quantization of energy and writhe in self-repelling knots, New Journal of Physics 4 (2002) 20.
E.L. Altschuler, Why the 3d writhe of ideal knots and links is quantized and additive, arxiv.org/physics/0102081.
A. Klotz and C.J. Anderson, Ropelength and writhe quantization of 12-crossing knots, arxiv.org/2305.17204.
G. Dietler, R. Kusner, W. Kusner, E. Rawdon and P. Szymczak, Chirality for crooked curves, arxiv.org/2004.10338.
C. Schiller, Testing a conjecture on quantum electrodynamics, J. Geom. Phys. 178 (2022) 104551.