●
● Prize list F:
Favourite strand challenges and prizes offered for their solution
● Prize list A: Prizes offered for
solving teaching challenges (volumes I to V)
● Prize list B: Prizes offered for special
achievements (volumes I to V)
● Prize list C: Prizes offered around the strand model (volume VI)
● Prize list D: Prizes offered for graphics and animations
● Prize winners for previous challenges
● Possible Theses and Papers
● Prizes for testing Ai systems with physics unification -
and for distinguishing them from charlatans
The six volumes of the free physics text contain over 1700 challenges in physics and maths. Some solutions are not included. For challenge solutions of particular didactic or research value I offer special prizes. The first good solution I receive will be added to the free physics textbook, together with the sender's name. Partial prizes may also be awarded. To apply for a prize, mail a solution to christoph@motionmountain.net. Prize list B is for special achievements. Several challenges from prize lists C and F could lead to publications, form chapters in a PhD thesis, or both.
Note: do not submit anything if you used Ai systems anywhere in or for your submission. Such submissions are not acceptable and not accepted, except for those listed here. Sapere aude!
All prizes are for the first solution sent in. (Der Rechtsweg ist ausgeschlossen.).
MAIN PHYSICS PRIZES: Invitations to Dinner
This prize list is for special achievements in the foundations of physics. Because the prizes are probably unachievable, there will also be prizes for interesting aspects and for interesting attempts, even if unsuccessful.
First Dinner Challenge: Discover new physics, i.e., physics beyond the standard model with massive neutrinos, and you will receive an invitation to dinner. For the hundreds of ways to get food, see this numbered list. However, there have been no invitees, requests for invitation, or candidates since the year 1973.
Second Dinner Challenge: Observe any new deviation from general relativity or any new quantum gravity effect, thus any effect apart from elementary particle masses, mixing angles or coupling constants, and you will receive an invitation to dinner. However, there have been no invitees, requests for invitation, or candidates since the year 1930.
Third Dinner Challenge: Observe any new trans-Planckian effect or observe any new variation over space or time of any fundamental constant or of any Planck unit - elementary particle masses, mixing angles, coupling constants, c, G, ℏ or their combinations - and you will receive an invitation to dinner. However, there have been no invitees, requests for invitation, or candidates since the year 1905.
Fourth Dinner Challenge: Provide a new argument against the fundamental principle of the strand tangle model - the "tiny theory of motion", and you will receive an invitation to dinner. This includes any new argument against the 9 lines, any argument requiring new physics, and any alternative, inequivalent approach to unification that agrees with experiments. However, there have been no invitees, requests for invitation, or candidates since the year 2008.
Some potential discoveries or arguments can fall into several categories. They will then lead to several invitations.
Since 2008, four invitations have been won, all for interesting arguments. One is for Tejinder Singh for his octonion unification approach. One is for David Wiltshire, for his calculations that eliminate the need for dark energy and dark matter. One is for Subir Sarkar, for his measurements rejecting dark energy and confirming David Wiltshire's approach. A fourth invitation is private.
PRIZE LIST F: Favourite strand challenges and prizes offered for their
solution:
Challenge F 3: Determine, using the tangle model, the mass ratio between the neutrinos and the electron. Prize: 500 €. The result is worth publishing.
Challenge F 4: Determine, using the tangle model, a better approximation for the fine structure constant than 1/126. Prize: 500 €. The result is worth publishing.
Challenge F 5 (partially solved): Determine how the probability of belt-trick-like rotation for a polymer-tethered ball depends on the chirality and size of the ball and on the number of polymer chains. First, look at this video. Then, imagine that each belt is exchanged by two parallel cylindrical polymer chains, and that there are not only 4, but 2n of them; also imagine that the central buckle is a chiral structure. In the strand model, the probability for the belt trick is related to the absolute mass of the elementary particles. So solving this polymer problem in detail will also advance particle physics. The solver will receive a special prize plus an amount of at least 500 €. The result is worth publishing.
Challenge F 6: Falsify any of the over one hundred experimental strand predictions, with experiments or other arguments. The prize will be substantial. Please write to set terms together. The result is worth publishing. Even if you do not write, the head of the experiment will get a dinner invitation.
Challenge F 7: Prove, clarify or disprove this conjecture: no visualization of SU(2) or SU(3) without tethers is possible in 3 dimensions. Prize: 50 €. The result is worth publishing.
Challenge F 8: Prove, clarify or disprove this conjecture: no non-equivalent visualization of SU(3) to the one with three strands is possible in 3 dimensions. (A triangular belt buckle with three attached belts attached with hinges does not count as "inequivalent".) Prize: 50 €. The result is worth publishing.
Challenge F 9: Prove, clarify or disprove this conjecture: no visualization of SU(n) with strands for n > 3 is possible in 3 dimensions. (This would have profound consequences for physics, including the lack of GUTs.) Prize: 50 €. The result is worth publishing. Here, a visualization is any model that uses 3d structures.
Challenge F 10: Prove, clarify or disprove this conjecture: no visualization of SU(n) with n > 3 is possible in 3 dimensions, of any kind. Prize: 50 €. The result is worth a publication. Here, a visualization is any model that uses 3d structures.
Challenge F 11: Prove, clarify or disprove this conjecture: the rational tangle classification is mathematically complete and leaves no room for additional elementary fermions or bosons. (This clarifies the options for dark matter.) Prize: 150 €. The result is worth a publication. The proof shall also explain what
Challenge F 12: Prove, clarify or disprove this conjecture: the rational tangle classification is mathematically complete and leaves no room for additional defects in space that are neither fermions nor bosons. (This clarifies the options for dark energy.) Prize: 50 €. The result is worth a publication. A way to allow or eliminate one-dimensional defects or wormholes should be part of the argument.
Challenge F 13:
Prove, clarify or disprove this conjecture: the
3d writhe or some other chirality measure of rational 3d tangles is quantized
(similar to that of knots) and determine the size of the
writhe quantum for 3d tangles. Prize: 200 €. The result
is worth a publication. I would help in writing the paper.
(Note: For ideal, i.e., tight knots, 3d writhe is quantized in (certain) multiples of 1/7.
Maybe the number of strands plays a role in the quantization of 3d writhe.
Maybe the 3d writhe of a tight rational 3d tangle is proportional to 2d writhe.
It is sufficient to provide a solution only for alternating tangles, or
only for tangles made of two
or three strands given in Figure 25 in the preprint
Testing a model for emergent spinor wave functions
explaining gauge interactions and elementary particles.
Challenge F 14: Deduce the Gårding-Wightman axioms, or the Osterwalder-Schrader axioms, or the Haag-Kastler axioms of quantum field theory from the strand tangle model. Prize: 50 €. The result is worth a publication.
PRIZE LIST A: Prizes offered for solving teaching challenges (volumes I
to V)
Challenge A 2: The 'tangles inside a sphere' problem. This problem combines topology, statistics and geometry. Estimate the number of topologically different tangles that can fit into a sphere of given volume, with the assumption that every strand, though flexible, has constant diameter. A glass sphere of radius R contains n strands of diameter d (d<R), all starting and ending on the surface (at 2n given and fixed points distributed over the surface). How many topologically different tangles can be formed, under the condition that the diameter d has the largest possible value for a given n? [Note: in mathematics, one distinguishes trivial, composed, rational, locally knotted and prime tangles. The problem asks for the number of possible tangles that are composed or prime. Locally knotted tangles may be left out of the counting; rational tangles do not count as topologically different in this problem.] Prize: 1000 € – and publish the solution! One attempt so far.
Challenge A 3: Classical Lagrangian for waves. Use the relation for the errors in angular frequency and time for wave packets, dw dt > 1/2, to show that the classical action for a wave is bounded below. Find the precise bound by assuming that the initial and final points for which the action is determined must themselves obey the wave packet relation. Prize: 100 €. The result should be published.
Challenge A 4: Rotation in special relativity. Make a movie of a sphere/football with relativistic speed and relativistic rotation speed. Show the strange effects that appear. Prize: 100 €. The result should be published. Half an attempt so far.
Challenge A 5: The simplest unsolved knot problem. Imagine an ideally wobbly rope, that is, a rope that has the same radius everywhere, but whose curvature can be changed as one prefers. Tie a trefoil knot into the rope. By how much do the ends of the rope get nearer? In 2011, there are only numerical estimates for the answer: about 10.1 diameters. There is no formula giving the number 10.1 yet - can you find one? Alternatively, solve the following problem: what is the rope length of a closed trefoil knot? Also in this case, only numerical values are known - about 16.33 rope diameters - but no exact formula. Prize: 500 € from me, plus eternal fame. The result should be published. Two attempts so far.
Challenge A 6: Extending the belt trick to spin 3/2. The Dirac belt trick simulates the behaviour of a spin 1/2 particle. What is the construction for a composed spin 3/2 particle? For an elementary spin 3/2 particle? Prize: 50 €. One attempt so far.
Challenge A 7: Taking a combined photograph of a rainbow, similar to the one by Stefan Zeiger, but including a third segment with the ultraviolet picture. Prize: 50 €.
Challenge A 8: Explain the problems in performing a Bohm-type experiment with two nuclei that are first near each other and then separated. Prize: 50 €.
Challenge A 10: Supply valuable details on the mathematics of tree growth: the laws about their proportions, the height of their trunks, as derived from the principle of minimum effort, etc. Prize: 50 €. Two attempts so far.
Challenge A 12: Provide figures of the most important topological defects: twirls, hedgehogs, etc. Prize: 10 €.
Challenge A 15: Supply beautiful and clear photos for wave interference, polarization, diffraction, refraction, wave damping, and wave dispersion. Prize: 20 € each.
Challenge A 16: Write an article about the site and book in a newspaper or journal. Prize: a paper edition.
Challenge A 18: Take and send in pictures or films about striking examples of motion in biology or in any other field - with permission of use. Prize: 50 €.
Challenge A 19: Propose good solutions to challenges marked as "ny". Prize: 10 € each.
Challenge A 20: Propose counter-examples to maximum force, maximum power, or maximum mass flow. Prize: 200 € for valid ones, 10 € for false, but good ones.
PRIZE LIST B: Prizes offered for special achievements (volumes I to V)
Challenge B 1: Propose substantial improvements to the text. I will reward your input in a way that is comparable to the other rewards listed here.
Challenge B 3: Translate untranslated parts of the text into Spanish, Italian, German, French or any other language. Click here for details on how to do it and then let me know. I will find a way to reward your efforts appropriately.
PRIZE LIST C: Prizes offered for challenges about the strand
model (volume VI)
Challenge C 2: Determine the probability of twists (Reidemeister Type I moves) for a chiral tangle made of two or three strands. Show that the square of the probability is 1/137.036. Prize: 1000 €. The result is worth a publication.
Challenge C 3: Determine, from the strand model, how the mass of the W and Z bosons run with energy. Prize: 500 €. The result is worth a publication.
Challenge C 6: Deduce, using the strand model, an analytical approximation for particle mass ratios or particle masses. The approximation could be based on ropelength or on the W/Z mass ratio calculation - but does not have to be. Prize: 1000 €. The result is worth a publication.
Challenge C 7: Find, using the strand model, an analytical approximation for probabilities of core shape changes. Prize: 1000 €. The result is worth a publication.
Challenge C 9: Describe, for the strand model, the relation between strand distance and the modulus of the wave function. Prize: 50 €.
Challenge C 10: Deduce in a simple way, for the strand model or textbook quantum mechanics, Schwinger's quantum action principle from the quantum of action. Prize: 100 €. The result is worth a publication.
Challenge C 11: Find, for the strand model, a simple visualization of the weak mixing angle, also called the 'Weinberg angle'. Prize: 100 €. The result is worth publishing.
Challenge C 13: Describe, for the strand model, the precise phase choices for a crossing that lead to SU(3) invariance. Prize: 200 €. The result is worth publishing.
Challenge C 14: Visualize, for the strand model, the relation between SU(3) in the harmonic oscillator and SU(3) due to the third Reidemeister move. Prize: 200 €. The result is worth publishing.
Challenge C 15: Check the six basic lepton tangles and estimate their ropelengths. Prize: a surprise. The result is worth publishing.
Challenge C 17: Confirm or invalidate the new W and Z tangles defined with the help of strands. Prize: a surprise. The result is worth publishing.
PRIZE LIST D: Prizes offered for graphics and animations
Challenge D 2: Produce animations about the
spinning tangles of quarks, leptons and certain bosons
in Shadertoy, with the same look as in Challenge D1 (but coloured),
and without the errors (write me first) visible here:
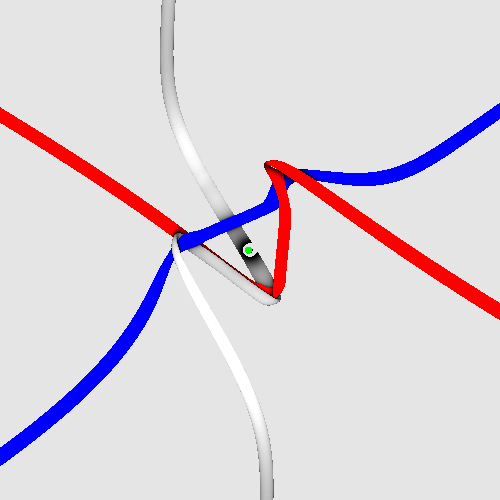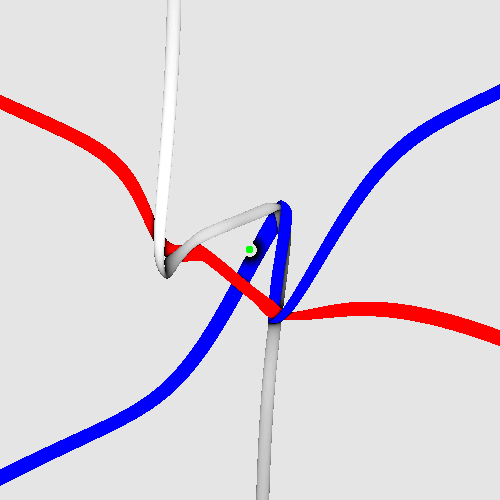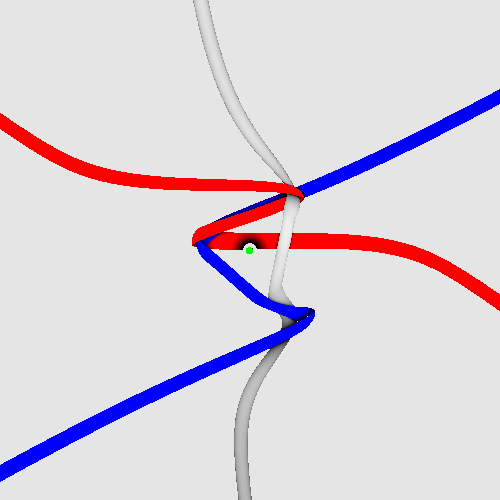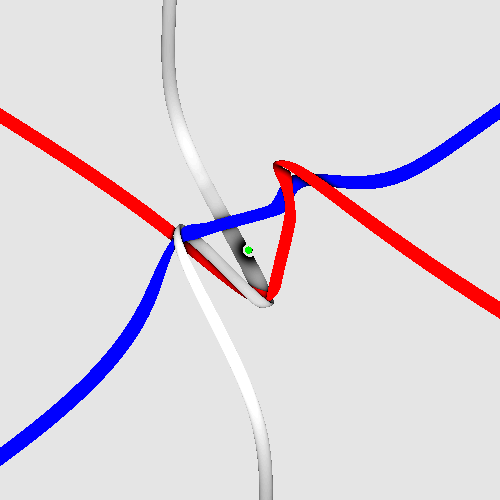Spinning electron.
Evolving photon.
Prize: 50 € for each quark and for each lepton, 30€ for the photon.
The animations will be used in publications, on Twitter, Mastodon and on
these web pages.
Challenge D 4: Produce animations about
the three gauge groups U(1), SU(2) and SU(3) in Shadertoy, based on the top of
Figures 5, 6 and 8 shown in this paper.
(They should be 3d interactive, to allow different observation directions.)
An example (Figure 6) would be these three animations:
Details and prize are to be discussed together. The result will be used in publications,
on Twitter, Mastodon and web pages.
Challenge D 5: Produce an animation (if possible in
Shadertoy, but this is not required) about the origin of wave functions
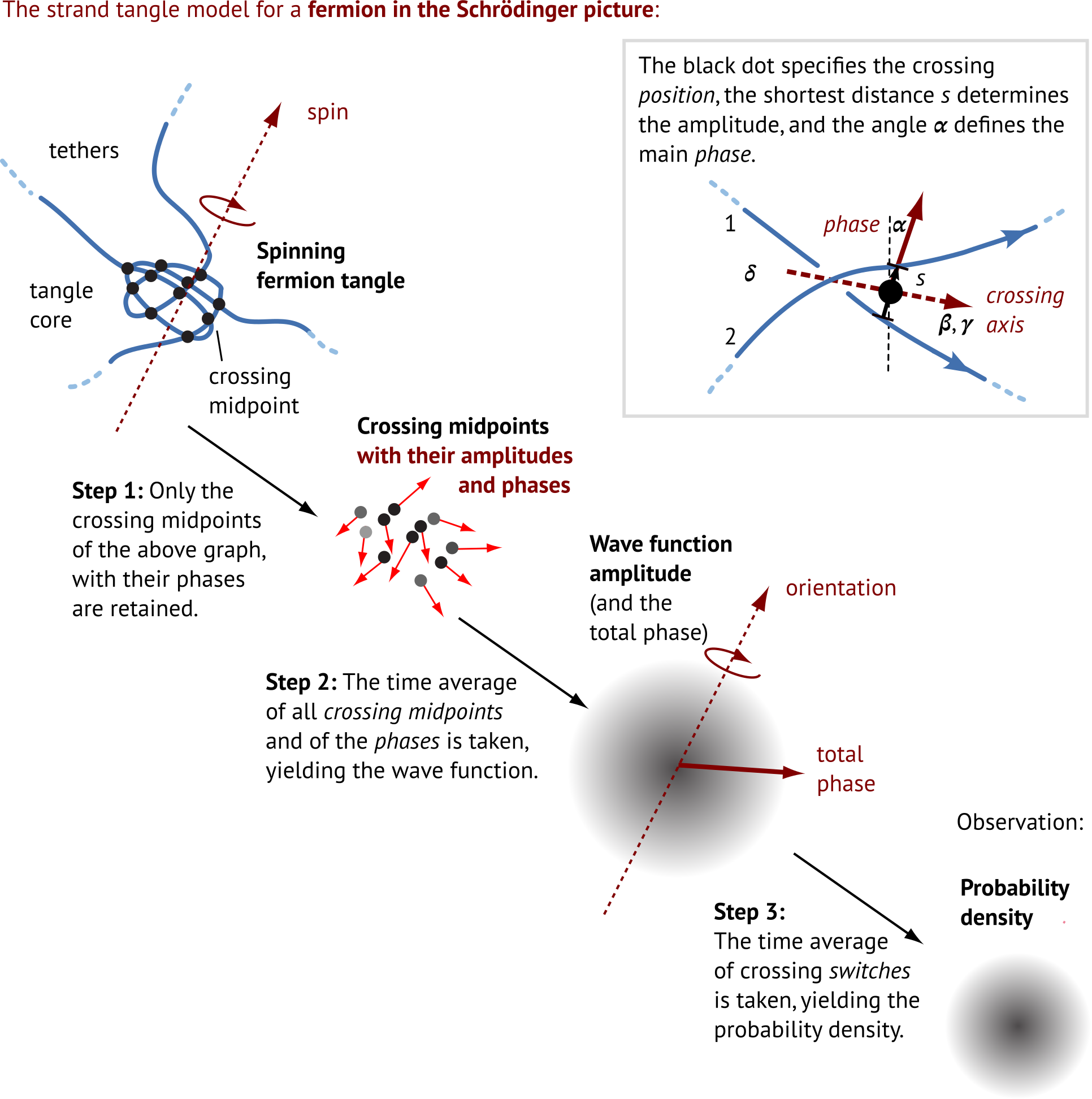
Prize: to be decided.
The result will be used in publications, on Twitter, Mastodon and on web
pages.
Challenge D 6: Produce animations about the gauge interactions and the Higgs interaction in Shadertoy, based on challenge D4. (They should be 3d interactive.) Details and prizes are to be discussed together. The result will be used in publications, on Twitter, Mastodon and on web pages.
PRIZE WINNERS for previous challenges
Solved challenge A 1: The parking problem. Find the minimum number of times one has to drive backwards and forwards to leave from a parking space, when the available space and the geometry of the car are given. Look up the details by searching for 'car parking' in the book index. After several attempts by others, the prize has been awarded to Daniel Hawkins.
Solved challenge A 9: Convince Adobe to eliminate an ugly and old bug: in Adobe Reader, horizontal lines are shown on screen irregularly in usually exaggerated thicknesses. That makes tables look horrible. The bug has been noted and communicated to Adobe by many since version 1 of the program; it is still present in version XI. This one will receive a special reward because even several Adobe engineers gave up on the topic in the past three times. (The reward was 50 € plus a paper copy of the 6 volumes signed by the author, with a special thank you letter in the name of all graphics artists worldwide.) Now solved by Adobe; nobody claimed the prize.
Solved challenge A 11: Provide a research literature reference for the diffusive speed of light in the solar interior. Prize awarded to Zach Espiritu.
Solved challenge A 13: Send in a quality CAD drawing of a Foucault gyroscope. Prize also awarded to Zach Espiritu.
Solved challenge A 14: Take and send in a beautiful and clear photograph of how a candle flame reacts to a rubbed comb or, better, of how it splits in a high electric field. Prize awarded to Shubham Das and Rakesh Kumar.
Challenge A 17: Find a research literature reference for the difficulties encountered when trying to observe classical tachyons, i.e. the difficulties encountered when a classical tachyon (assuming it exists) flies across your field of view. (There is a better reference than Recami, somewhere, I know it from hearsay. There is also a website somewhere, I saw it and lost it in 2014.) Prize awarded to Aleksandr in 2025.
Solved challenge A 20: Produce an animation that is unique throughout the world, one that shows clearly how two belts behave as fermions under exchange, complementing the now standard visualisation that a belt behaves like a fermion under rotations. Together with the usual belt trick, the animation would thus visualize the spin-statistics theorem for spin 1/2. The ideas and the original physical behaviour to be shown are straightforward, but the graphic work will take a bit of patience. The resulting animation would extend the applet shown at http://www.gregegan.net/APPLETS/21/21.html to a situation with two belt buckles and four belts. If you are interested, get in touch with me. One option could be to start with the software at www.cs.indiana.edu/~hansona/quatvis/Belt-Trick/index.html and then expanding it. The resulting animation will be unique worldwide, and I would build it into the text. The prize goes to Antonio Martos for his wonderful animation.
*
Solved challenge C 4: Extrapolate the measured up and down quark masses to Planck energy, using the standard model. Solved by Shun Zhou.
Solved challenge C 8: Formulate, for the strand model, a simple relation between strand diameter and the Planck time. Solved in the new edition of volume VI.
Solved challenge C 12: Find, for the strand model, a compelling deduction of the gluon tangles. Solved in the new edition of volume VI.
Solved challenge C 16: Calculate or estimate the ropelength of the (corrected) Higgs tangle (volume VI). Solved by Eric Rawdon and Rob Sharein.
*
Solved challenge D 1:
Produce animations about the three
Reidemeister moves in Shadertoy, with the look shown here.
An example is: 
Solved by Ben Kilgore. See here.
Solved challenge D 3:
Produce an animation about the fundamental principle, if possible in Shadertoy,
with the look of Challenge D1, but showing this process:
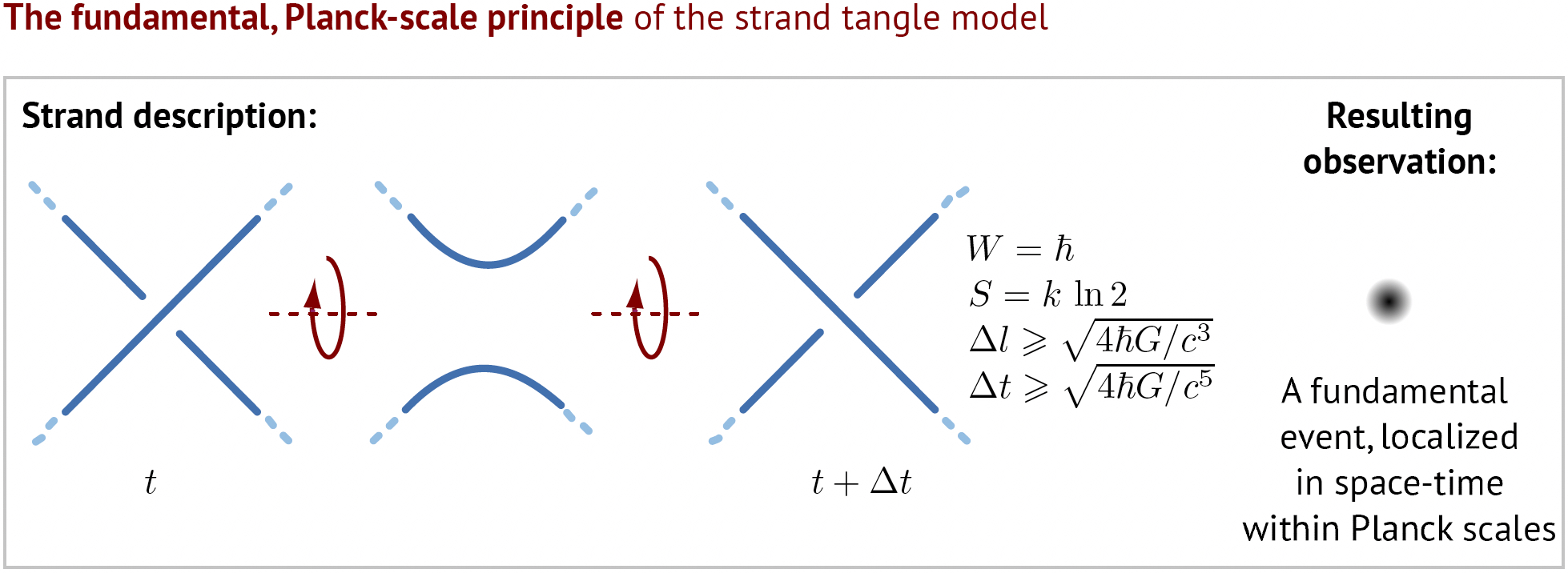
Solved by Ben Kilgore.
*
Solved challenge F 1: Discover the correct tangles, in volume VI, for the leptons. Solved in 2018.
Solved challenge F 2: Draw a 3d picture in eps format of space-time curvature and allow me to use it in the text. Solved in 2018 by Farooq Ahmad Bhat.
Solved challenge F 13: Prove, clarify or disprove this conjecture (not really related to strands): the local value c^4/4G is an upper limit. Prize: 50 €. The result should be published. Solved and published in PRD Phys Rev D 104 (2021) 124079.
Possible Theses and Papers
Elementary particles and topology
* Prove, clarify or disprove that the rational 3d tangle classification is mathematically complete and leaves no room for additional elementary fermions or bosons.
* Prove, clarify or disprove that the rational 3d tangle classification leaves no room for additional defects in space that are neither fermions nor bosons.
* Hard: Determine how the probability of belt-trick-like rotation for a tethered ball depends on the chirality and size of the tethered structure and on the number of ropes. Use ideas from hydrodynamics of viscous liquids. Use the result to estimate all elementary particle masses.
* Hard: Determine the neutrino masses using the tangle model. Ideally, before they are measured.
* Produce, using the tangle model, a useful animation of a spinning electron tangle. Improve this one. Relate the new animation to the topics and the puzzles from this page, including the g-factor.
Gauge theory & topology
* Prove, clarify or disprove that there is no visualization of the Lie groups SU(2) or SU(3) without tethers, possibly using the ideas of Shapere and Wilczek.
* Prove, clarify or disprove that there is no visualization of any additional Lie groups at all, using tethers.
* Hard: Determine the three gauge coupling constants to high precision. Find a tangle chirality measure for each charge.
* Hard: Determine the g-factor of the electron to high precision.
* Produce, using the tangle model, a pedagogically valuable and useful animation of photon emission, inspired by the puzzles from this page. Relate the animation to the puzzles on that page.
Quantum theory and quantum optics
* Model entanglement measures and entanglement entropy with strands. Compare bit threads and strands.
* Confirm that tangles explain Hall's arXiv:2406.13040 on shocking quantum correlations and Mermin's paper on his Bell's equation demonstrator.
* Deduce Schwinger's quantum action principle from strands in an elegant and pedagogically valuable way.
* (Done) Confirm that ħ is due to crossing switches and that no other option is possible at the Planck scale.
* (Done) Confirm that all uncertainty relations are due to the non-commutativity resulting from strands and tangles.
* (Done) Explain pedagogically unitary and hermitian operators with strands.
* (Done) Confirm that tangles are skeletons of wave functions.
* (Done) Confirm that tangles model quantum entanglement.
* (Done) Visualize entangled photons, as used in Aspect's experiments, using strands. Write a pedagogical paper visualizing all properties of photons using strands.
Gravitation and cosmology
* Prove with additional arguments and in full detail that black hole mass is distributed over the horizon, and not concentrated at its centre or anywhere behind its horizon.
* Prove that there are no wormholes.
* Hard: Estimate the cosmological constant from strands, including its time dependency or lack thereof. Check whether it is non-vanishing. Relate it to Wiltshire's ideas.
* Hard: Find a way - or prove its nonexistence - to deduce MOND from the tangle model for gravity. Relate the tangle model to Verlinde's ideas. Relate it, in particular, to Wiltshire's ideas.
Weak nuclear interaction
* Hard: Find, with the strand model, a pedagogical visualization of the weak mixing angle, also called the Weinberg angle. If possible, find an estimate.
* Write a paper with the title “Testing a conjecture on the weak interaction” similar to the publications “Testing a conjecture on quantum electrodynamics” and “Testing a conjecture on quantum chromodynamics”.
* Confirm or invalidate the W and Z tangles.
* Estimate the quark mixing angles using the tangle model.
* Estimate the neutrino mixing angles using the tangle model.
* Quantify the Higgs mechanism, maybe using the leather trick.
Prizes for testing Ai systems with physics unification - and for distinguishing them from charlatans
Challenge Ai1: Naturally intelligent systems know that mathematical research is not easy. Test your Ai system by asking: "Can you find a formula telling by how much the ends of a long rope of radius 1 get closer when you tie a tight overhand knot into it?" If your Ai system is the first to solve this famous unsolved geometry problem, the so-called ropelength problem, I will invite you to dinner.
Challenge Ai2: Naturally intelligent systems know that physics research is not easy either. Test your Ai system by asking: "Can you explain the origin of the value of the fine-structure constant?" If your Ai system is the first to deduce the origin of the number 137.0359991(1) with all its digits (or any other coupling constant), I will invite you to dinner.
Challenge Ai3: A further test of your Ai system: "Can you explain the origin of the value of electron mass?" If your Ai system is the first to find out the origin of the electron mass with all measured digits, or of the mass of any other elementary particle to all measured digits, or of their mixing angles and phases, I will invite you to dinner.
However, there are many reasons to conclude that such results will not arise in the coming years. A few such reasons follow, partly triggered by the unified description of motion presented on this site.
Ask your Ai system: "What is the biggest unsolved problem in fundamental physics?" or "Which observed phenomenon is still unexplained?" So far, no Ai system answers correctly. No Ai system seems to know the correct answer given by Pauli, Dirac, and Feynman. Ai systems cannot distinguish what is important from what the mass of people talks about. (Solution: see here.)
Ask your Ai system: "Can you generate a hypothesis on quantum gravity that agrees with all observations about nature?" The answer shows that many present Ai systems are essentially stochastic parrots with little comprehension of concepts, with no ability to generate hypotheses or to compare hypotheses with observations. The better systems can be called Absent innovation systems – with an uppercase "A" and a lowercase "i" – the worse ones word salad systems.
Ask your Ai system about some of the mistakes of physics researchers since 1973 to check how good it is. For example, ask your Ai system: "Why did the search for the unification of physics take so long?" or "Is there a world formula?" (The answers: Insisting on using points to describe particles and space cannot lead to unification. Because the minimum length implies that points do not exist in nature, there is no world formula.)
Ask your Ai system "Do general relativity and quantum mechanics contradict each other?" (The answer: there is a theoretical contradiction, but no experimental proof for such a contradiction, because all alleged contradictions only arise in trans-Planckian domains, which do not exist in nature.)
Intelligence is seen first of all in the clarity of the used concepts and the reasoning. Test your Ai system by asking: "Is there any change in nature that is not motion?" (The answer should be: No.)
Distinguishing lies and nonsense from physics and science is simple: doubt and check. Doubting means to ask why? and to evaluate the arguments. A 'check' is a comparison with observations. If doubting or checking a statement is impossible or not allowed by some authority, the statement is wrong, thus it is at least nonsense and at worst a lie. For example, any claim that nature has secrets is a lie. Nature does not hide anything. Likewise, any claim about hidden energy, faster-than-light travel, other or previous universes, or alien technology is a lie. Nature does not hide knowledge or laws. Nature is accessible to everybody. Test your Ai system by asking: "Is science opposed to authority?" (Answer: yes, always.) "Is there a sizeable zero-point or vacuum energy?" (Answer: no.)
Test your Ai system further by asking "Is nature made of information?" (Answer: No, because nature has a smallest length and length measurement error, so that nature, at its foundations, is fuzzy and is not made of bits.)
Test your Ai system by asking: "Can facts be checked?" (Answer: Statements can be doubted and checked, but facts cannot. The expression 'fact-checking' is a lie. Worse, fact-checkers are self-declared authorities. Science is opposed to lies and authorities. Every statement in physics can be doubted and checked. By everybody. Including you.)
Naturally intelligent systems know: physics, like every natural science, collects precise, unambiguous statements about observed motion. Test your Ai system by asking: "Is physics the science of motion?" (The correct answer is: "Yes.")
Test your Ai system by asking: "Is a correct theory of everything possible?" Naturally intelligent systems know: the more sensational the name of a theory, the more wrong it is. The term 'grand unified theory' is used for a group of older research approaches that were neither grand, nor unified, nor theories. The expression 'final theory' has always been reserved for titles of mediocre books and games. Expressions starting with 'super...' are used for unsuccessful attempts from the past. The expression 'world formula' has never been correct; it is reserved for misleading theatre plays – and for calculating the optimal way to park a car backwards. The term 'theory of everything' is mostly used for unsuccessful esoteric healing attempts and for titles of mediocre films. There cannot be a 'theory of everything'; there can only be a unified description of motion.
As long as your Ai system answers the question "Is there a minimum length in nature?" by saying that the question is not settled, it does not have any reasoning skills. (The correct answer is: "Yes, the double Planck length.") The same applies to the question: "Is there a minimum length measurement error in nature?"
Likewise, as long as your Ai system answers the question "Which effects of relativistic quantum gravity have been measured so far?" by saying "none", it does not have any reasoning skills. (The correct answer is: "The observed relativistic quantum gravity effects are the gauge interactions, their Lie groups, the coupling constants, the spectrum of elementary particles, their quantum numbers, their masses and their mixing constants - and the principle of least action.")
Ask: "Is gravity a force?" or "Does the Earth go around the Sun?" or "What is the cosmological horizon?" or "Is there a singularity inside a black hole?" or "What is inside a black hole?" or "What is the moment of inertia of a Schwarzschild black hole?" and then "If it is finite, how can the mass be in a central singularity?"
Together, the answers show that despite claims to the contrary, no present Ai system is at the level of a professional physicist. At present, in 2026, no Ai system differs much from a well-read physics charlatan. No system correctly answers the question "What is the biggest unsolved problem in fundamental physics?" Ai systems are built to be sycophants. Thus, no present Ai system is useful as a discussion partner or as a collaborator. This is especially the case for questions about fundamental physics.
Above all, no Ai system is - and never will be - an authority in matters of fundamental science. We need to recall that science is opposed to authorities. Sapere aude - have the courage to use your own reason and your own thinking.
* * *