Strands provide a simple and correct explanation for wave functions.
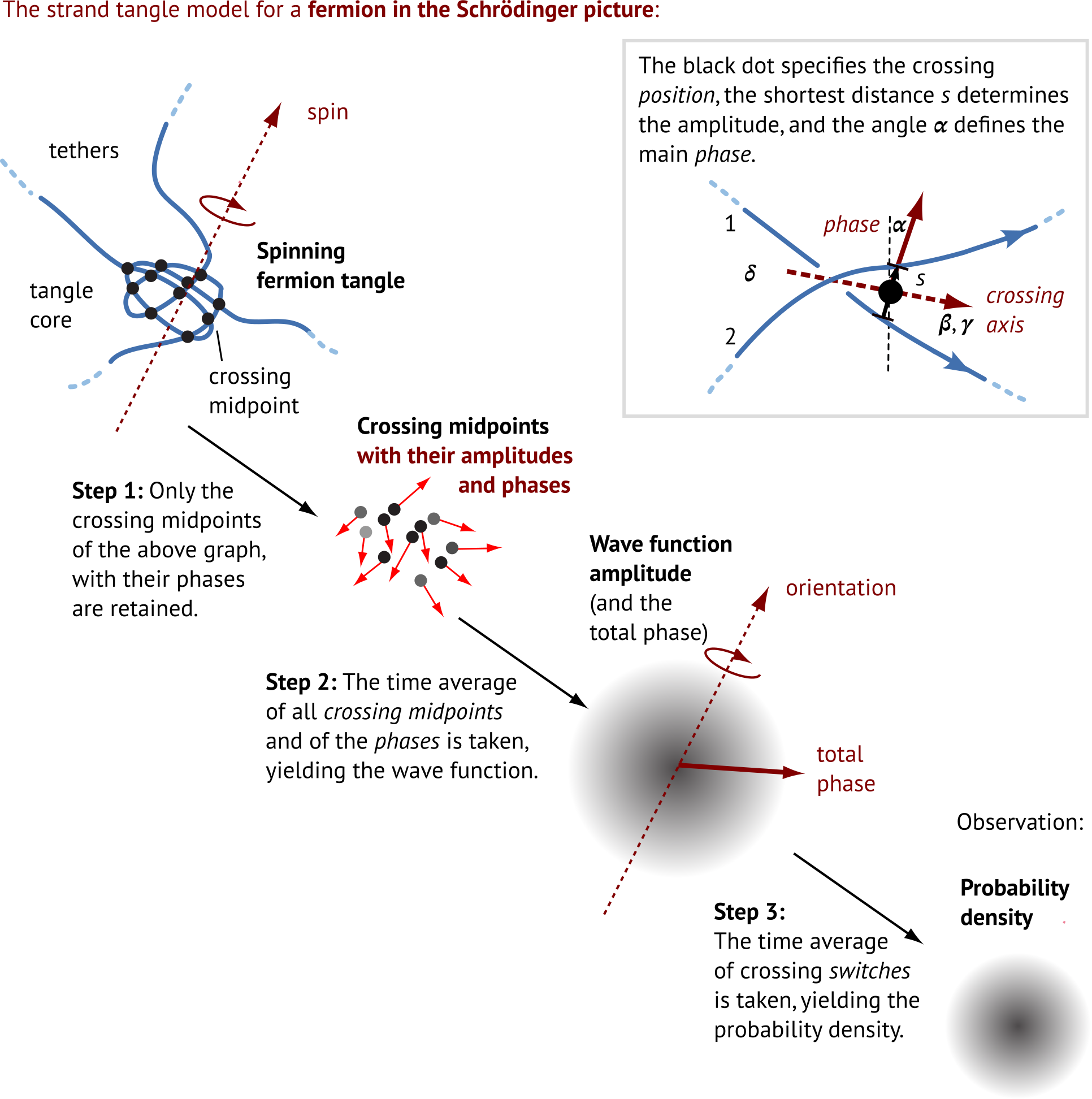
Wave functions are oriented crossing densities of fluctuating particle tangles.
Tangle topology determines the particle type. Tangle shape determines the
particle state. In other words, tangles of strands with Planck radius
visualize quantum theory:
2025 Slides:
How come the quantum? Testing Kauffman's topological origin for the
quantum of action
Slides:
An emergent model for wave functions explaining
gauge interactions and particle physics
Talk recording here.
Strands are special:
Testing the uniqueness of a unified description of motion.
● Overview of strand quantum theory
● Testable predictions of strand quantum theory
● Qubits
● The fascination of strand
quantum theory
● Similar ideas by other authors
● Bets and future tests
● Publications on quantum
theory from strands
Visual summary of strand quantum theory
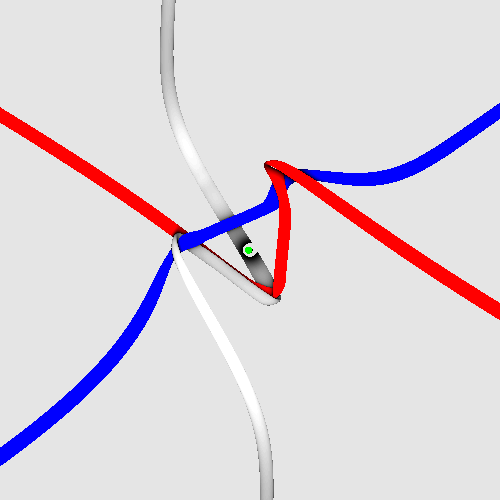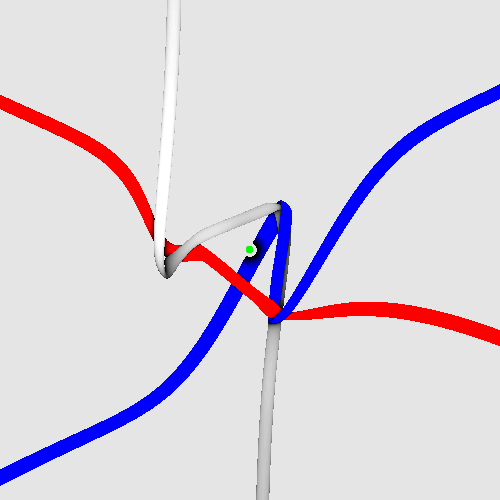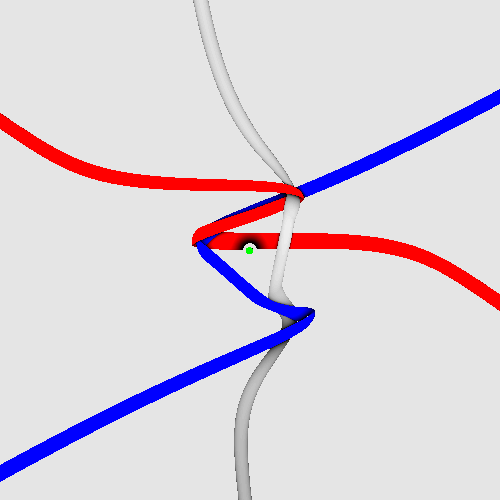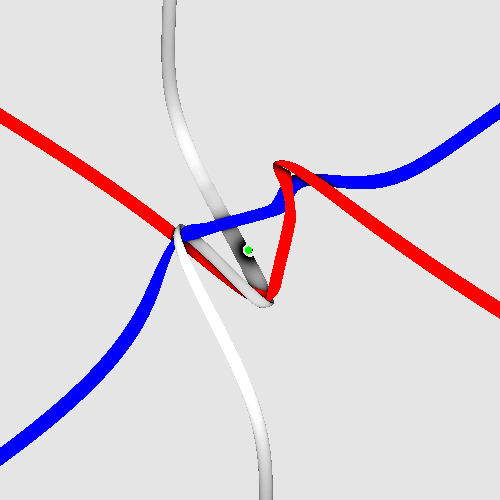
The spinning electron before blurring.
Three strands with Planck radius reproduce spin 1/2, fermion behaviour,
electrical charge 3 x 1/3 = 1, chirality, extremely low dipole moment,
small mass, vanishing colour charge, correct g-factor, correct antiparticle
properties, as well as correct gravitational, electromagnetic, weak and
strong interactions.
More graphics here.
Overview of strand quantum theory
Strands provide a Planck-scale model of particles that includes wave functions:
Wave functions are crossing densities of fluctuating and spinning tangles of strands of Planck radius. Tangles are rotating skeletons of wave functions.This strand tangle model allows deriving, from a single principle, the Schrödinger equation, the Pauli equation, the Klein-Gordon equation and the Dirac equation. The strand tangle model explains spin 1/2, fermion behaviour, countable particles, antiparticles, particle-antiparticle mixing, and particle mass values.
Elementary fermions are rational (braided) tangles of strands made of two or three strands.
For example, it is well-known that spinors behave like flags with a sign. (This corresponds to the analogy that vectors behave like arrows.) A tangle of strands indeed behaves like a flag: it has a direction for the pole (the direction in which the tangle core points, the spin orientation) and has an orientation of the flag (the phase, i.e., the orientation of the core around the pointing direction). In addition, the tangle also contains the sign that all spinors contain: positive if the tethers are untangled, negative if they are tangled.
Several consequences of the strand tangle model go beyond quantum theory. Classifying the possible tangle structures determines the possible elementary particles, their quantum numbers, their mass values and the Higgs mechanism. Classifying tangle deformations with the Reidemeister moves determines the possible gauge interactions, their symmetry groups and their coupling constants. Over 50 precision tests are deduced. All tests predict the lack of physics beyond the standard model with massive Dirac neutrinos. All tests agree with observations.
The strand tangle model is simple, unique, consistent, complete, and predictive. Strands imply that the standard model of particle physics is final and beautiful.
The pedagogical preprint linked above explains and shows that wave functions evolve deterministically, but emerge as the average of fundamental strand fluctuations. As expected from observations, wave functions are shown to have objective existence. Wave functions have a unique history. They have no hidden variables, despite appearances. Wave functions collapse. The environment, interacting baths and the measurement apparatus play a role. The measurement problem is solved by decoherence.
Also another result of quantum theory remains valid: the universe as a whole has no wave function and no Hilbert space. The "wave function of the universe" is a contradiction in terms: wave functions define the state for observations by outside observers. But there is nothing outside the universe - by definition.
Testable predictions of strand quantum theory
Lepton masses small. They are at least 17 orders of magnitude smaller than the maximum mass of elementary particles.
The Higgs mass is limited. It is at least 10 orders of magnitude smaller than the maximum mass of elementary particles.
There are no measurable deviations from the free Dirac equation.
Neutrino masses have normal order.
No physics beyond the standard model or beyond general relativity occurs.
No trans-Planckian effects of any kind occur.
There are no higher (or lower) dimensions.
In nature, there is an upper limit on probability density, given by the inverse smallest volume - but the limit cannot be reached.
There is no supersymmetry. Dark matter is not made of unknown elementary particles.
Glueballs exist.
Fundamental constants – elementary particle masses, mixing angles, and coupling constants – can and will be calculated.
Qubits
Strands also visualize qubits. The preprint introduces the topic.
Strands provide a way to visualize the statement by Zizzi about nature: it from qubit. Indeed, everything arises from qubits; more precisely, everything arises from crossing switches of strands.
The fascination of strand quantum theory
Strand tangles are skeletons of wave functions. Wave functions are crossing densities.
Measurement and collapse are triggered by baths; collapse time is decoherence time and is short but measurable, in agreement with data.
Every electron, every atom, every basketball and every person is tethered.
Everything is connected to everything else.
The universe consists of a single strand.
Strands imply that `every thing' is made of `everything'.
Strands explain the fine structure constant and the electron mass. Thus they explain all colours around us.
Because strands have Planck radius and are unobservable, they are not hidden variables.
Similar ideas by other authors
So far, apart from the work by Battey-Pratt and Racey (and Dirac's lecture demonstration), no similar ideas are found in the literature. Not even the researchers working on emergent quantum theory published anything similar. Several additional research papers that are close to the strand tangle model are cited in the pdf linked above.
Studying the complement of strands, i.e., the evolution of the space between them, could provide an equivalent alternative, as done by Asselmeyer-Maluga. However, his model has not yet achieved a classification of particles or interactions, nor deduced a model for wave functions – though this should be possible.
Tests and bets
In science, every statement must be checked continuously, again and again, against observations. This is ongoing. A sweeping statement like "strands crossings explain wave functions" must be checked with particular care. If you have a counterargument or notice a missing issue, just send a note to the author.
The numerous experimental predictions, tests and proposed bets (click here) are extremely precise. They cover all domains of nature and of physics. So far, all tests for the strand model are positive. Finding a single observation falsifying a single prediction of the strand tangle model wins the bet.
Finding any alternative, correct and inequivalent description of wave functions – or of nature – wins the bet as well.
A provoking consequence: all approaches claiming that space is continuous and all approaches claiming that space is discrete are mistaken.
It might be that the similarities between strand gravity and strand particle entanglement can be used to deduce connections between gravity and entanglement.
An interesting aspect is the following: experiments with tethered chiral bodies in slowly flowing liquids or gases should yield estimates for particle mass values.
In the past, models for quantum theory have not been successful. The whole topic has a mixed reputation. But if one does not risk making a fool of oneself, there is no progress. Therefore: enjoy exploring strands and enjoy exploring their relation to quantum theory.
Publications on quantum theory from strands
This simple introduction for mathematicians, physicists and physics
students explains the origin of wave functions and the gauge groups U(1), SU(2)
and SU(3): C. Schiller, On the relation between the three
Reidemeister moves and the three gauge groups
International
Journal of Geometric Methods in Modern Physics (2023) DOI:
10.1142/S0219887824500579. Download the
preprint here.
*
The exploration of quantum electrodynamics also introduces wave
functions arising from strands:
C. Schiller, Testing a conjecture on quantum
electrodynamics,
Journal of
Geometry and Physics 178 (2022) 104551.
Download the preprint
here.
* * *