The strand conjecture provides a simple explanation for the origin of the three gauge interactions in nature – and for the absence of any other gauge group.
Slides showing how tangles and the three Reidemeister
moves lead to the three Lie gauge groups and the unification of physics
Talk recording in English here.
Nederlandstalige versie hier.
Preprint explaining why strands are special:
Uniqueness of the unified description of motion.
● How strands lead to gauge symmetry
● What is quantum field theory?
● Testable predictions of
strand gauge theory
● Publications
Summary: gauge theory from strands
Strands allow deriving, from the single fundamental principle, the three observed gauge theories. More precisely, strands explain that the three gauge groups U(1), broken SU(2), and SU(3) are due to the three Reidemeister moves. Strands do not allow any other gauge group.
Strands prove that the standard model of particle physics is unique, complete and beautiful.
How strands lead to gauge symmetry
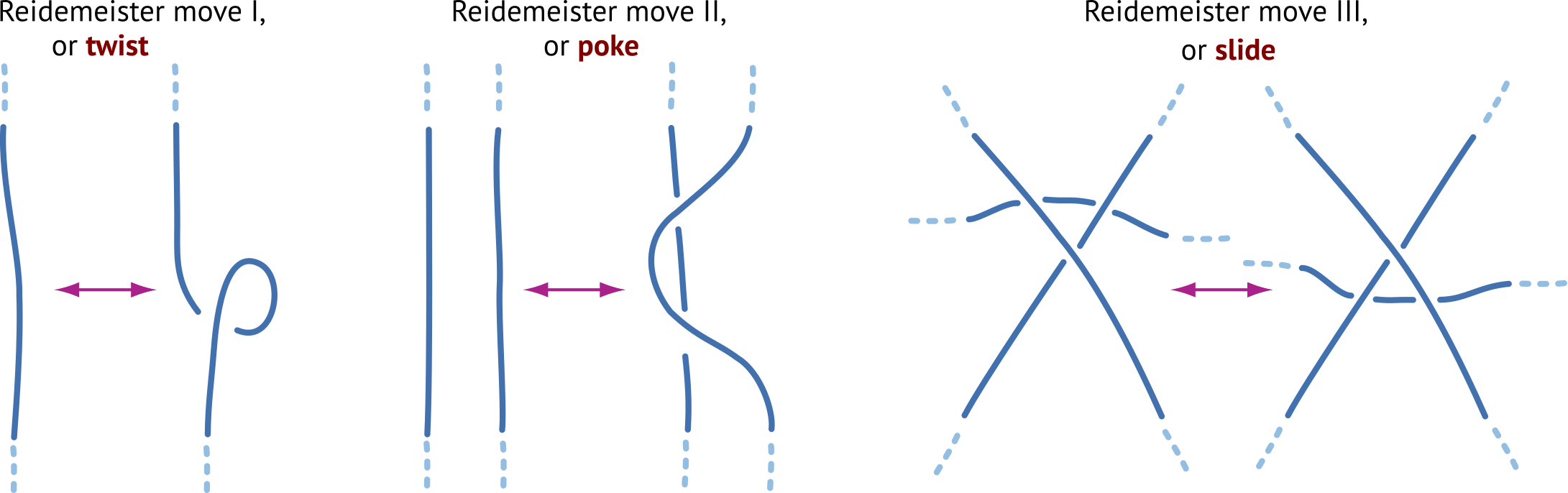
In nature, only three gauge symmetries are observed: U(1) for electrodynamics, broken SU(2) for the weak interaction, and SU(3) for the strong interaction. In the tangle model of particles, gauge symmetries are due to strand deformation in the particle core. Deformations can be classified; this is done by the so-called Reidemeister moves. The main discovery is: Each Reidemeister move corresponds to a gauge group.
In nature, gauge symmetry is due to the freedom to define particle phase. In the tangle model of particles, gauge symmetry is due to the same freedom. The particle phase is defined with the help of strand crossings. Every crossing has the same properties that particle states, i.e., wave functions, also have. Wave functions are explored on a separate page.
The first Reidemeister moves, the twists, generate U(1),
the second Reidemeister moves, the pokes, generate SU(2),
and the third Reidemeister moves, the slides, generate SU(3).
These are the main properties of strand deformations.
The animated Reidemeister moves, by Ben Kilgore. Just click.
Because there are only three Reidemeister moves, there are only three gauge groups. This connection solves all questions about gauge theories. Strands imply that there is no other gauge group, in particular, no grand unification and no supersymmetry.
What is quantum field theory?
In the strand conjecture, a quantum field is a loose, fluctuating tangle that is made of strands with Planck radius.
The fluctuations of the tangle crossings, averaged over time, produce probability densities. The tangle topology fixes the particle type and its quantum numbers. The tangle model allows producing extended, continuous fields, and the counting of discrete particles at the same time. The tangle model automatically yields indistinguishable, identical particles. The tangle model reproduces spin and statistics, as well as their connection.
The tangle model implies that particles are countable and localized excitations of the (untangled) vacuum: the excitation is the tangling. The tangle model reproduces particle creation by tangling, particle annihilation by untangling, particle absorption by tangle combination and particle emission by tangle separation. Vacuum excitations lead both to particles and to antiparticles. The tangle model also implies that particles can transform into each other: different tangles can be combined and single tangles can be separated into two tangles.
The tangle model implies that interactions are deformations of tangles. The tangle model implies that interactions are local - within Planck dimensions. The tangle model implies that the interaction spectrum is limited, by the Reidemeister moves, to the three known gauge groups of the standard model. The tangle model implies that the weak interaction violates parity, breaks SU(2), and violates CP invariance, in contrast to the electromagnetic and the strong interaction. The tangle model implies that fermions mix, described by unitary mixing matrices. The tangle model implies that couplings are unique and run with four-momentum.
From tangles to quantum electrodynamics
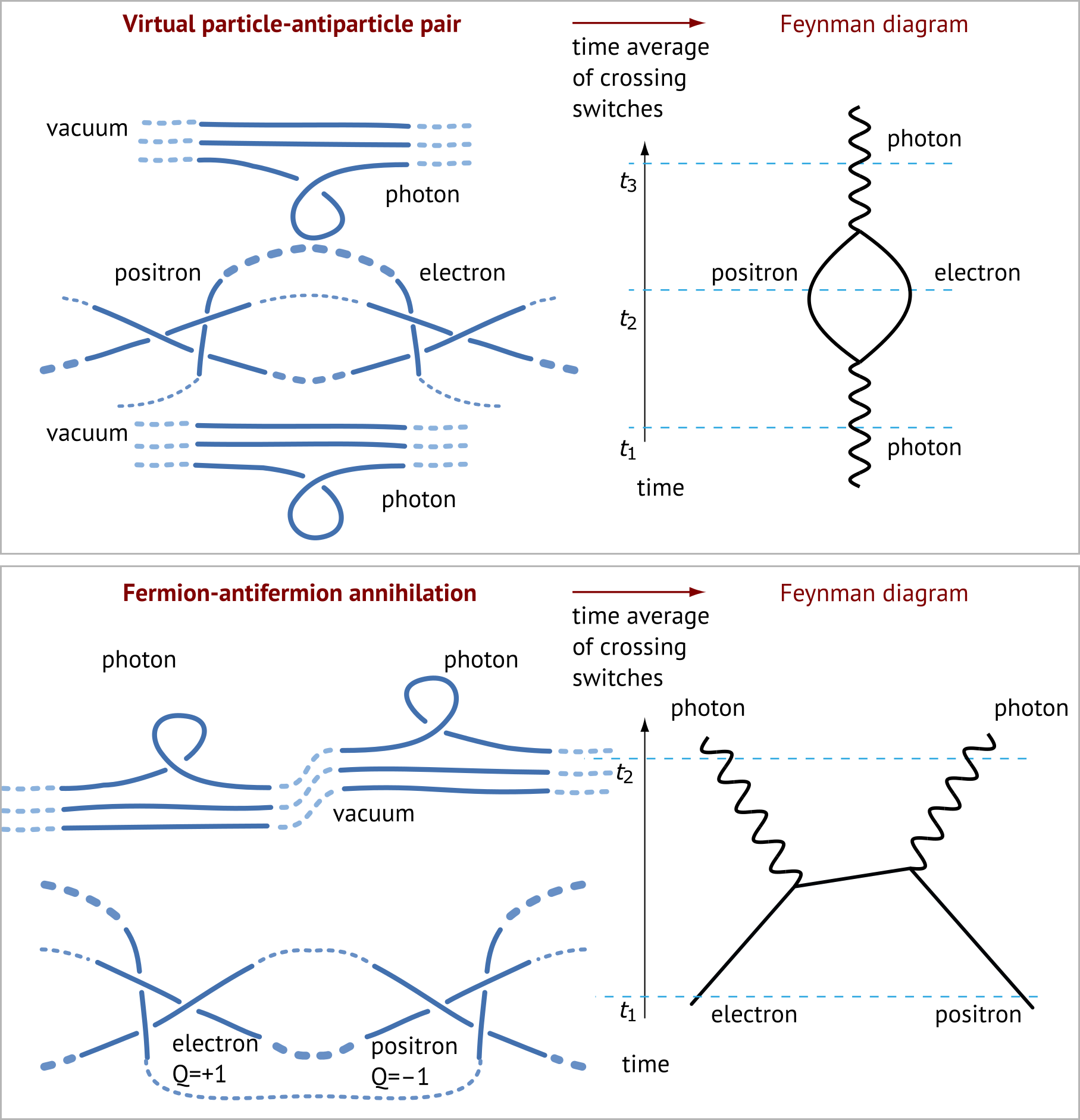
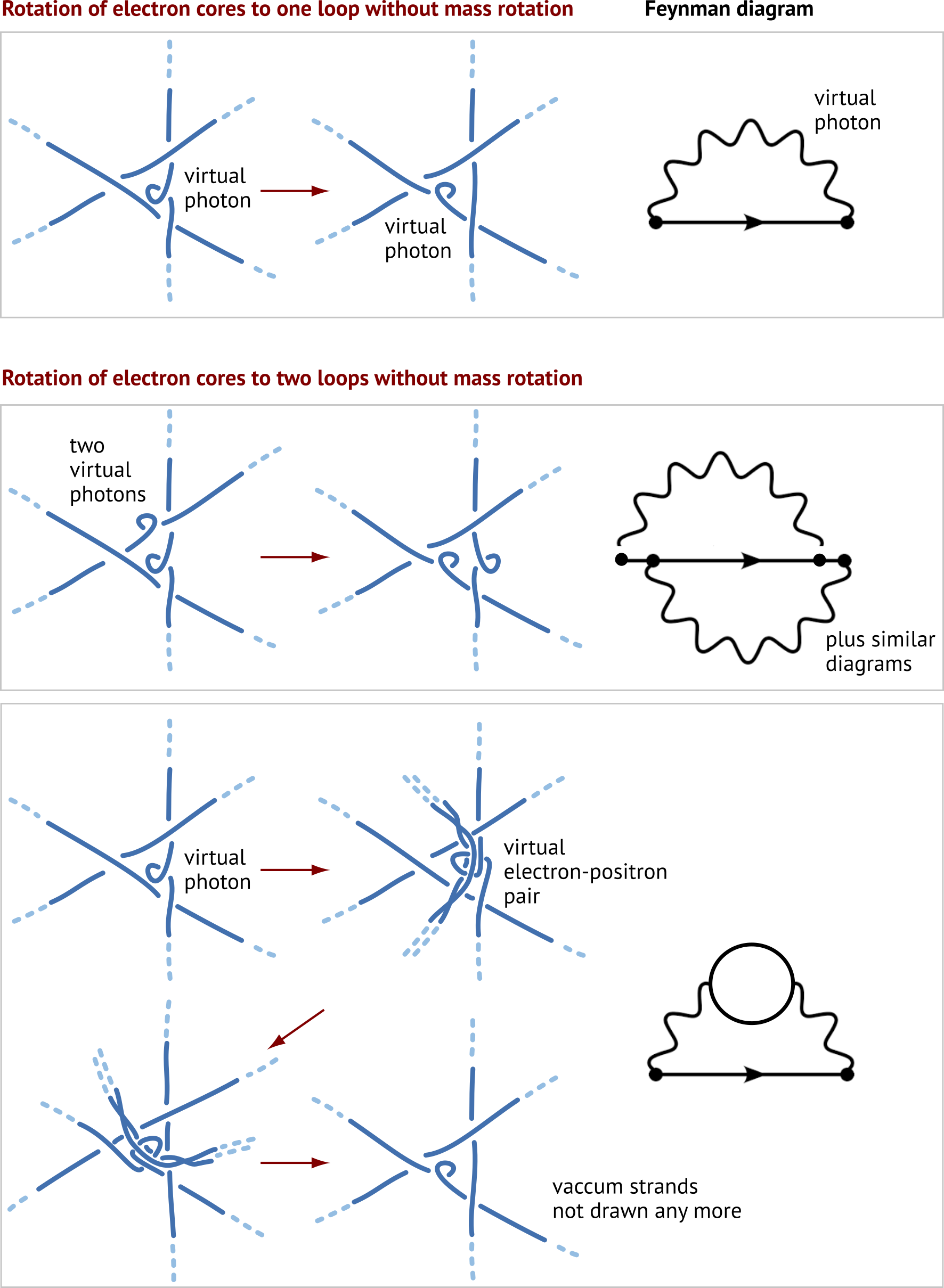
The tangle model implies the same perturbation expansion as conventional quantum field theory. The tangle model implies that perturbation expansions are due to more complex tangles arising at small scales.
The tangle model implies that quantum fields have a Lagrangian and follow the principle of least action. (This eliminates all quantum field theories without Lagrangians.) The tangle model implies that couplings are weak. The tangle model implies that the standard model is renormalizable: tangles allow at most quadruple vertices. The tangle model implies that quantum fields have an (unusual) strong coupling regime - in the tangle cores. The tangle model implies that quantum fields have an approximate duality between strong and weak coupling - but not an exact one. The tangle model implies that quantum fields have topological aspects - but are not topological quantum field theories. The tangle model implies that space is (approximately) continuous, but not non-commutative or fermionic or discrete. The tangle model of elementary particles is free of anomalies because the standard model is. The tangle model provides the desired argument explaining why: the lack of anomalies is due to the topology of the elementary particle tangles and to a particle spectrum resulting from tangle classification.
The tangle model implies that there is a natural cut-off at the Planck scale. The tangle model implies that there is a well-defined continuum limit. The tangle model also implies that all observables are local - within Planck dimensions. The tangle model implies that observables obey axiomatic quantum field theory - within Planck dimensions and limits.
The tangle model implies that physical space has three dimensions at all scales, that there is only one vacuum state and that flat empty space-time is Lorentz-invariant.
Any counter-example to any of the statements above directly invalidates the strand conjecture.
The Feynman vertices of the standard model
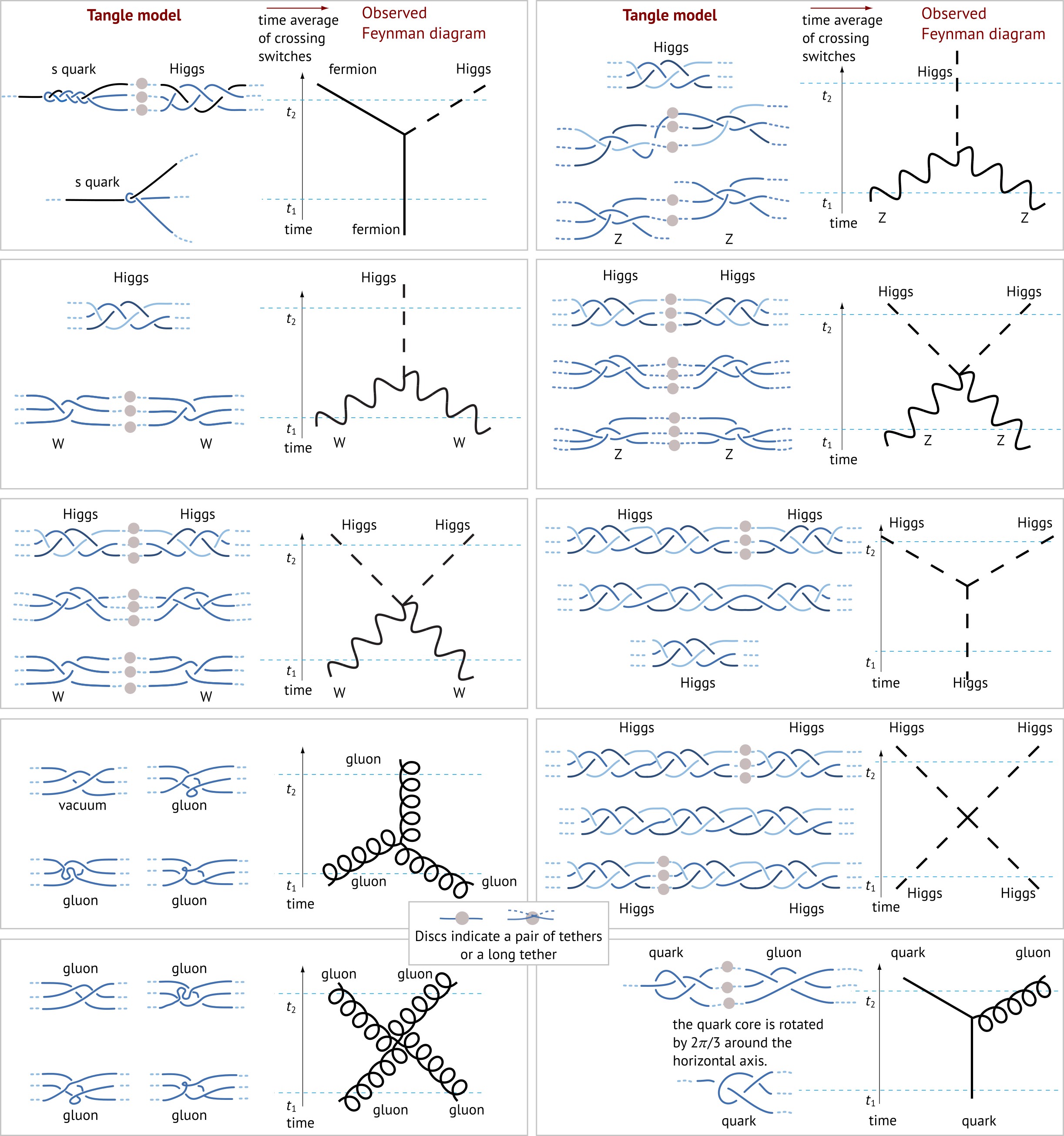
Testable predictions of strand gauge theory
Strands provide a simple explanation of the observed gauge groups U(1), broken SU(2), and SU(3). Strands explain the origin of gauge symmetry and of gauge groups.
There is no other explanation that agrees with experiments.
There is no other explanation that eliminates other possible symmetries.
There is no other, equally simple explanation in the literature.
There is no other explanation ab initio.
The strand explanation is consistent. The gauge groups arise as consequences of the same idea with which Dirac explained spin 1/2, with which Battey-Pratt and Racey explained the Dirac equation, with which the field equations of general relativity arise, and with which the entropy of black holes can be deduced.
The strand explanation is complete. Strands also determine the particle spectrum, the fundamental constants, and general relativity. No question remains unanswered.
The strand explanation is predictive. Additional gauge groups, additional dimensions, additional particles, additional interactions, additional symmetries - be they local, global, discrete, supersymmetric, or non-commutative - and additional energy scales are all not possible in nature. Above all, values for the fundamental constants that differ from the observed ones are not possible. In other words, the tangle model does not allow generalizations. This feature of a quantum field theory is unusual, but it is required and expected from any unified model.
All predictions can be summarized in a single statement: there is no physics whatsoever beyond general relativity and beyond the standard model with massive Dirac neutrinos with PMNS mixing.
In science, every statement must be checked continuously, again and again. This is ongoing. A sweeping statement like "strands explain gauge theory, quantum field theory, and allow no modification" must be checked with particular care. Everybody is invited to check it. If you have any potential counterargument or notice a missing issue, just send a note.
More detailed and specific experimental predictions are listed here. Finding any single observation falsifying the strand conjecture or the standard model, or just finding an alternative, correct and inequivalent description of gauge theory – or of nature – falsifies the model.
So far, it appears that the strand explanation and derivation of gauge theory is unique, simple, ab initio, consistent, complete, predictive and correct.
The weak interaction
The three gauge interactions observed in nature are due to the three Reidemeister moves.
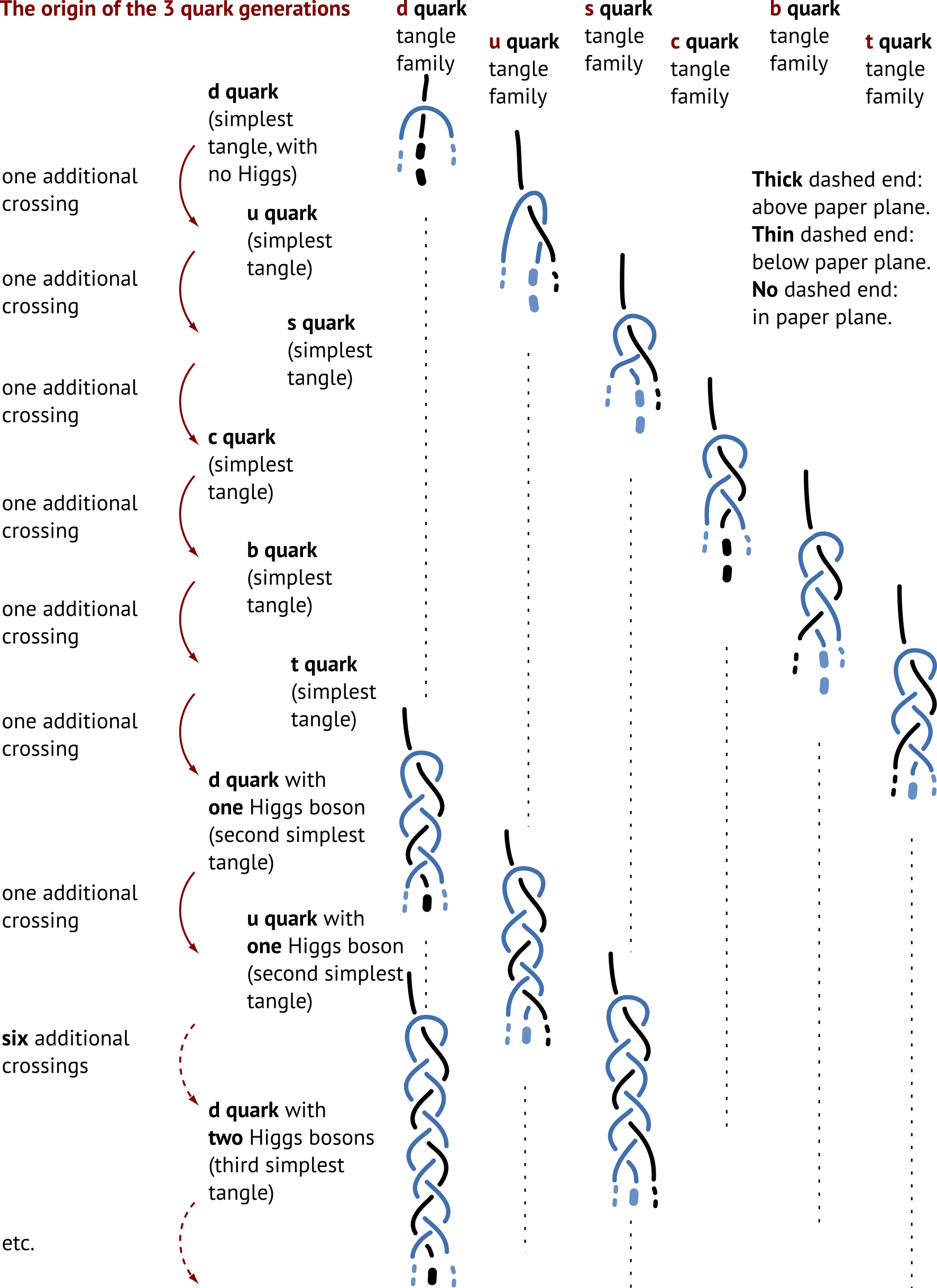
The weak interaction differs from the other two interactions both topologically and physically: the weak interaction can effectively change the topology of a particle. In experiments, the effect is called mixing. In particular, mixing allows changes of quark type (or "flavour"). Topologically, mixing corresponds to a tail exchange, thus to a second Reidemeister move whose second half occurs "far away."
In this way, a tail exchange due to the weak interaction explains every rational 3d tangle made of two strands. This is an example of a more complex tangle:
Such a tangle appears in higher-order Feynman diagrams of the weak interaction. (It is extremely short-lived.) Similarly, using tail exchanges, all 3d tangles consisting of two strands can be derived from the six quarks. Furthermore, the six quarks are related among themselves by tail exchanges. This relation is observed and is called "weak mixing".
The topological description of tail exchanges as an effect of the weak interaction includes the interaction with the Higgs boson. This interaction is a special case: it is a process in which 6 alternating tail exchanges are added.
Indeed, in nature, the Higgs and the weak interaction are closely related. The Higgs leads to a periodicity in the definition of the quarks. The Higgs therefore influences the mass values of all particles with which it interacts.
In a similar manner, the weak interaction can also change the flavours of the neutrinos, which are made of three strands. Topologically, neutrino mixing means to rotate three of its tethers against the other three. This is visible in their tangles:
Given that elementary fermions almost surely can only consist of two or three strands and that their tethers have to be equally distributed in space, it is claimed that the six quarks and most probably the six leptons are the only possible elementary fermions.
Publications
This simple introduction for mathematicians, physicists and physics
students explains the gauge groups U(1), SU(2)
and SU(3): C. Schiller, On the relation between the three
Reidemeister moves and the three gauge groups
International
Journal of Geometric Methods in Modern Physics 21 (2024) 2450057, DOI:
10.1142/S0219887824500579.
Download the
preprint here.
*
An exploration of quantum chromodynamics and the quark model was
published as C. Schiller, Testing a conjecture on quantum chromodynamics,
International
Journal of Geometric Methods in Modern Physics 20 (2023) 2350095, DOI:
10.1142/S0219887823500950. Download the
preprint here.
*
An exploration of quantum electrodynamics was published as
C. Schiller, Testing a conjecture on quantum
electrodynamics,
Journal of
Geometry and Physics 178 (2022) 104551.
Download the preprint
here.
*
A dedicated discussion of the strand description of the standard model was published as C. Schiller, Testing a conjecture on the origin of the
standard model, European Physical Journal Plus 136 (2021)
79. Download it at doi.org/10.1140/epjp/s13360-020-01046-8. Read the published paper online for free at
rdcu.be/cdwSI. Download the
preprint here.
*
The first publication on the strand model was C. Schiller, A conjecture on deducing
general relativity and the standard model with its fundamental constants from
rational
tangles of strands, Physics of Particles and Nuclei
50 (2019) 259–299. Download the published paper at
dx.doi.org/10.1134/S1063779619030055. Read the published paper online for free at rdcu.be/cdCK7.
Download the
preprint here, with films.
*
The first text that explained the relation between gauge groups and strands, in 2009, is available from arxiv as arxiv.org/abs/0905.3905.
* * *