Unifying physics – about the origin of colours and of the universe
This and the other pages with grey title stripe present the simplest unified description of fundamental physics that includes quantum gravity, general relativity and the standard model of particle physics, with massive neutrinos. This description, called the strand tangle model, is the only unified description for which all testable predictions and all consequences agree with all experiments. The description is inspired by ideas of Kauffman and Dirac. (My name is Christoph Schiller; I am a theoretical physicist and my biography is found on this page.)
The strand tangle model is daring in its ideas – every particle is connected to the cosmological horizon with unobservable strands – is complete in its coverage – from wave functions and quantum fields to the standard model, black holes, general relativity, cosmology and the fundamental constants – but is specific and restrictive in its experimental predictions: there is no new physics, but all fundamental constants can be calculated.
Fluctuating tangles of unobservable strands of Planck radius describe particles. Tangle crossing densities describe and visualize wave functions, field strengths, and quantum effects. Untangled strands describe empty space. Weaves of strands describe black hole horizons.
The strand tangle model describes all of nature with a single fundamental principle: observable crossing switches of unobservable strands explain and visualize quantum of action ħ and all other limits of nature, including the maximum speed c at the basis of special relativity, the maximum force c4/4G at the basis of general relativity, and the minimum entropy k ln 2 at the basis of thermodynamics. It is a truly tiny theory.
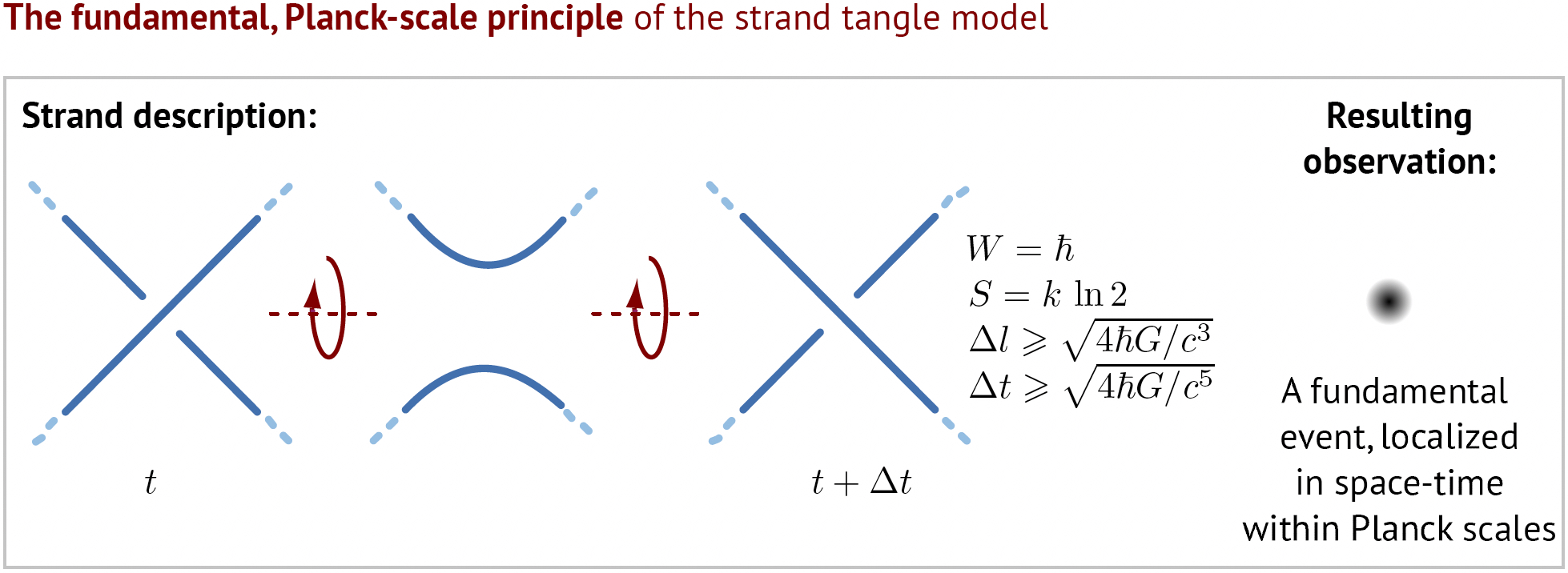
Nature and physics are due to fluctuating unobservable strands of Planck radius, for which every crossing switch yields Planck's quantum of action ħ, all other Planck limits, and thus all physical observables. As shown below, fluctuating strands imply the Hilbert Lagrangian of general relativity and the complete Lagrangian of the full standard model of particle physics, including massive neutrinos that mix.
In particular, for
the first time, unobservable strands explain the origin of wave
functions, the origin of the least action principle, the origin of the
three observed gauge interactions, the origin of the observed elementary
particles, the origin of all Feynman vertices, and the origin of all
particle properties, including their quantum numbers, masses, coupling
constants, and mixings. Strands predict, in numerous
details, the lack of any observation beyond the standard model with massive
neutrinos and beyond general relativity. In other words, strands agree
with all experiments ever made. Strands explain the origin of gravitation,
curved space and black holes. Strands explain all
motion and all laws of nature. Strands also provide a theory of quantum
gravity. Furthermore, the unified description of space, particles and
interactions with unobservable strands appears to be the only possible
one.
An introductory overview: the laughter of nature
These are the most recent presentations of the strand tangle model.
(Peer-reviewed publications are listed below.) The presentations show
how beautiful and simple nature is at the Planck scale. They are
written for physicists and physics students and they explain how space,
particle physics and general relativity follow from strands. Predictions
are clear and testable. An important intermediate result is the lack of
any equations and any Lagrangians describing nature beyond
general relativity and the standard model with massive neutrinos. No
further correct equations are possible. Our love for equations has
led us theoretical physicists astray. Nature has been laughing at our
failed attempts to find improved or even unified equations for quite a while.
Talk slides
on how strands imply particle physics and general relativity are here.
![]() The slides explain most aspects of the standard model with massive
neutrinos, and deduce what happens beyond it.
The slides explain most aspects of the standard model with massive
neutrinos, and deduce what happens beyond it.
Older talk slides
with an older introduction to the strand tangle model are here. ![]() The slides show, with animations and experimental predictions, how strands
provide a complete description of motion, explaining the origin of the fine
structure constant 1/137.0359..., the electron mass, and thus all colours.
The slides show, with animations and experimental predictions, how strands
provide a complete description of motion, explaining the origin of the fine
structure constant 1/137.0359..., the electron mass, and thus all colours.
A comprehensive list of experimental consequences, tests and
predictions is here.
A simple introduction to strands in 12
one-minute pieces is found here.
Pictures of the correspondence
between tangles and Feynman diagrams are here.
A compact introduction to the origin of the gauge groups is
here. ![]()
A motivating introduction for scientists and philosophers is
this essay.
![]()
For commented scientific publications and preprints, read further.
●
● Step 1: Maximum force– implies general relativity
● Step 2: From maximum force to
unification– requires strands
● Step 3: From strands to black holes, general relativity,
and quantum gravity
● Step 4: The strand
conjecture about wave functions and field theory
● Step 5: The strand tangle
model yields the standard model
of particle physics
● Step 6: Quantum electrodynamics deduced from strands
● Step 7: Quantum chromodynamics deduced from strands
● Step 8: Cosmology deduced
from strands– about dark matter and dark energy
● Outreach
● Acknowledgements
● Volume VI of Motion Mountain
● Strands in other languages
● Publication list
Summary: what happens beyond the standard model?
1. All observations and all equations of fundamental physics follow from crossing switches of fluctuating strands with Planck radius that reach the cosmological horizon. Strands yield the standard model with massive neutrinos and general relativity.
2. All fundamental constants – the number of dimensions, the coupling constants, the particle masses and the mixing angles – are unique and follow from the strand tangle model. They can be calculated.
3. Strands predict – like textbook physics does and like Bronshtein's physics cube does – that there are no trans-Planckian observations and thus no observations beyond general relativity. Strands also predict that there are no observations beyond the standard model with massive Dirac neutrinos. All experimental predictions and all consequences deduced from strands – listed in this page – agree with all experiments.
4. No observation remains unexplained in fundamental physics. Even the principle of least action follows from the fundamental principle of the strand tangle model.
5. Strands predict that no other, inequivalent model yields these results.
6. Particles are rational 3d tangles of strands, wave functions are blurred strand crossing densities, black hole horizons are blurred weaves of strands, space is made of blurred crisscrossing strands, curvature and gravity are due to inhomogeneous strands, and the three gauge interactions are due to the three Reidemeister moves of tangles of strands.
7. The main properties: One principle. Based on Lorentz invariance. Implies 3 dimensions. Deduces the 3 gauge interactions. Derives the 3 generations and the known elementary particles. Reproduces spinors and perturbative quantum field theory. Reproduces the standard model with massive neutrinos. Reproduces curvature and general relativity. Reproduces black hole entropy. Unifies general relativity and quantum theory. Makes testable predictions. Science, not fiction.
8. Everything we see is a consequence of the fundamental principle, as
animated by Ben Kilgore (just click):
9. The fundamental principle states: each strand crossing switch produces a quantum of action ħ. This principle allows deducing the complete standard model of particle physics, with massive neutrinos, and full general relativity. This includes deducing spinor wave functions, antiparticles, Dirac's equation, virtual particles, the gauge groups U(1), SU(3) and broken SU(2), electromagnetic fields, Maxwell's equations, QED, the nuclear interactions, QCD, the particle spectrum with its three generations, massive Dirac neutrinos, PMNS mixing, the Higgs mechanism, weak CP violation but strong CP conservation, the quark model, all Feynman vertices, and also curvature, the metric, Einstein's field equations, the Hilbert Lagrangian, and cosmology. The following sections present the details.
10. Strands fill all of nature, forming particles, vacuum and horizon. Strands continuously fluctuate and push each other. They describe and explain every change, every process, every observation, and every movement in nature.
11. Only strands explain the origin of spin, wave functions and spinors. Only strands explain the origin of the Dirac equation and the origin of the principle of least action. Only strands allow us to understand quantum theory. Only strands explain the origin of the three spatial dimensions, the origin of each gauge interaction with its gauge group. Only strands explain the origin of each elementary particle and its quantum numbers. Only strands allow deducing, without any possible alternative, both the Lagrangian of general relativity and the Lagrangian of the standard model with massive neutrinos.
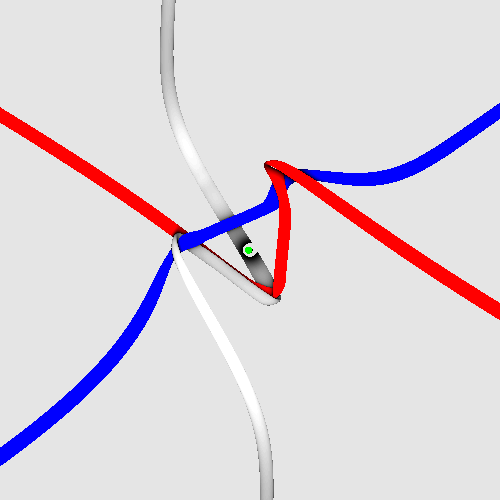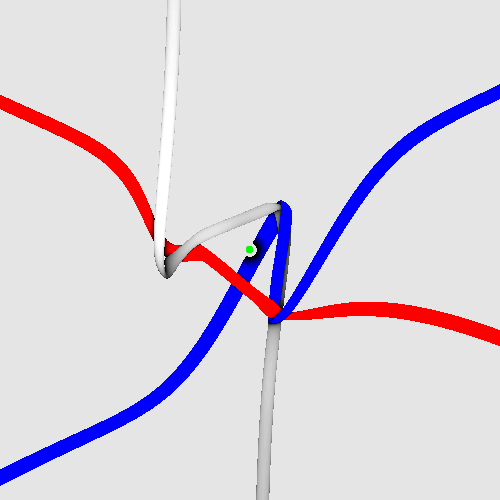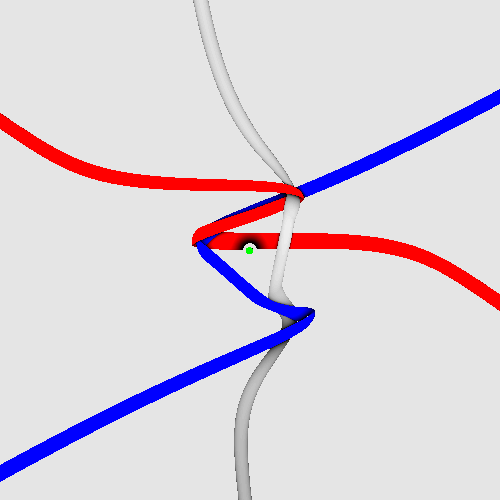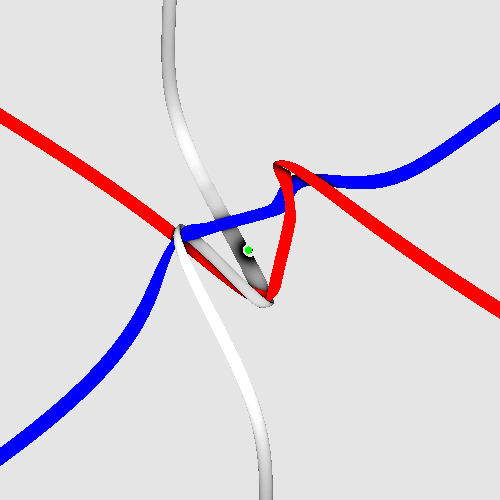 Spinning electron.
Spinning electron.
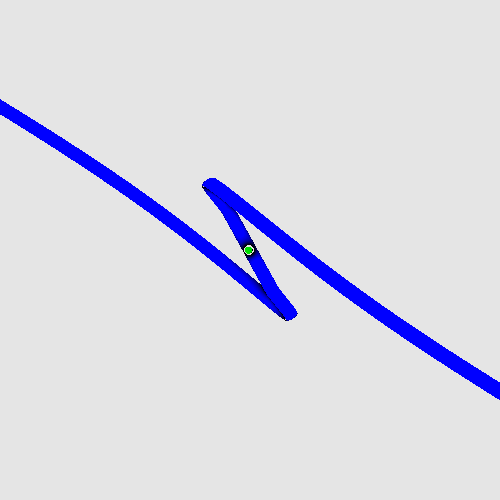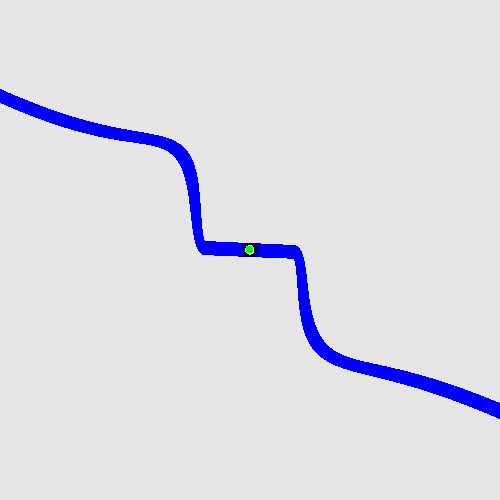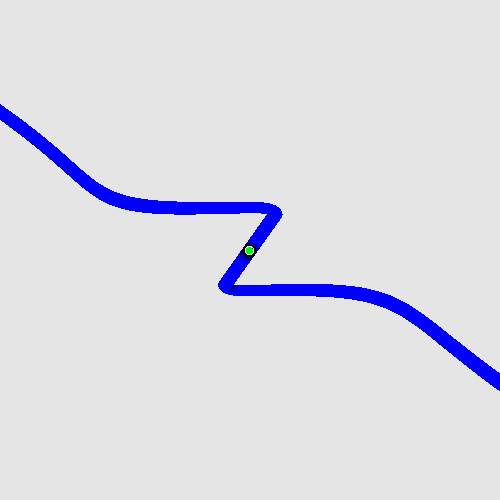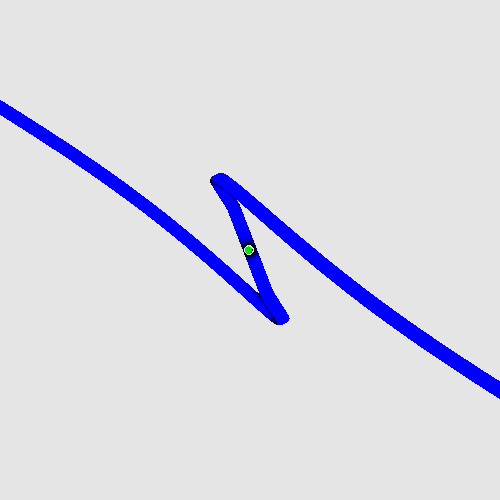 Evolving photon.
Evolving photon.
More here.
12. Finally, only strands explain the origin and uniqueness of each fundamental constant: particle masses – including neutrino masses – the fine structure constant, the nuclear coupling constants, and the mixing angles. However, their exact values still need more precise calculations.

Step 1: Maximum force
The story started with the discovery, in the years 2000 to 2003, of the maximum force value c4/4G in nature, by Gibbons and, independently, by the present author. In the past decades, a few papers tried to refute the result; over twenty papers by various groups across the world have confirmed it and corrected the apparent refutations. The author is also the discoverer of the principle of maximum force, i.e., of the result that general relativity can be completely deduced from nature’s limit c4/4G. The last papers by the author on the topic are
A. Kenath, C. Schiller and C. Sivaram, From
maximum force to the field equations of general relativity - and
implications,
International Journal of Modern Physics D 31
(2022) 2242019, 10.1142/S0218271822420196.
This paper won an honourable mention in the 2022
Competition of the Gravity Research Foundation.
Download
the pdf here. ![]()
C.
Schiller, Tests for maximum force and maximum power, Physical Review D 104
(2021) 124079. Preprint here.
![]()
C.
Schiller, Comment on "Maximum force and cosmic censorship", Physical Review
D 104 (2021) 068501
10.1103/PhysRevD.104.068501. Free preprint
here. ![]()
C. Schiller, From maximum force via the hoop conjecture
to inverse square gravity, Gravitation and Cosmology 28 (2022)
305–307, 10.1134/S0202289322030082.
Download the
pdf here. ![]()
All deduced results on maximum force c4/4G – or on the equivalent maximum power c5/4G, maximum mass flow rate c3/4G or maximum mass to length ratio c2/4G – agree with all observations so far, including those of the LIGO and Virgo collaborations, and of all neutron star and pulsar measurements. All these limits are equivalent; each one defines general relativity. For details, see the dedicated web page on maximum force and maximum power.
Step 2: From maximum force to unification with strands
The necessity to use strands to achieve unification
is deduced in simple terms in C. Schiller, From
maximum force to physics in 9 lines and towards relativistic quantum
gravity, ![]() published in Zeitschrift
für Naturforschung A (2022) https://doi.org/10.1515/zna-2022-0243.
published in Zeitschrift
für Naturforschung A (2022) https://doi.org/10.1515/zna-2022-0243.
A popular account has been published online in Essentia, in 2023.
A deeper dive towards unification with strands, still accessible to
every physicist, is the preprint
C. Schiller, From
the Bronshtein cube of limits to the degrees of freedom of relativistic
quantum gravity. ![]()
More preprints and presentations are available on Researchgate.
These texts make clear predictions on how to pursue unification, and deduce the lack of possible progress in most other directions. In particular, they summarize all experiments ever made and show that unification takes place in three spatial dimensions, unification must take into consideration the smallest length in nature, the double Planck length, and the fundamental, common constituents of space and particles must be filiform, fluctuating and of Planck radius. In short, the texts show that the fundamental constituents of nature must be strands.
Step 3: From strands to black holes, general relativity, and quantum gravity
The description of nature with strands reproduces the field equations and quantum gravity. This is shown in the following publications.
C. Schiller, Testing a conjecture on the origin of space, gravity and mass,
Indian Journal of Physics 96 (2022)
3047–3064. Read the published paper
online for free at rdcu.be/czpom. Dowload the
preprint here. ![]()
A dedicated discussion of the quantum gravity aspects of black holes
appeared as a chapter in the book by A. Kenath
ed., „A Guide to Black Holes“, Nova Science Publishers in January 2023:
C. Schiller, Testing a microscopic model for black
holes deduced from maximum force. ![]()
The first publication on gravitation from strands
was C.
Schiller, A conjecture on deducing general relativity and the standard
model with its fundamental constants from rational tangles of strands,
Physics of Particles and Nuclei 50 (2019) 259–299. ![]()
See also the dedicated page on quantum gravity.
50 756 solar masses per second. Strands provide a microscopic model for space and horizons. This allows deriving the field equations of general relativity and a model for quantum gravity. Numerous tests of the strand tangle model in the domain of gravitation and quantum gravity are deduced, starting from a single principle. All tests agree with observations so far.
For example, strands confirm that gravitation – like nature itself – has a power or luminosity limit c5/4G, a momentum flow or force limit c4/4G, a mass flow limit c3/4G, and a mass to length limit c2/4G. The limits are given by one quarter Planck mass per Planck time, or 50 756 solar masses per second (times c-1, times c, or times c2). No observation ever exceeded these limits.
Many predictions about gravitons and quantum gravity are deduced, including a direct derivation of black hole entropy from strands. Above all, strands also explain the existence of gravitational masses of elementary particles, solve the hierarchy problem, and provide upper and lower limits for the mass values. All predictions agree with the data.
Strands seem to be the simplest quantum gravity proposal in the literature. Strands agree with and predict all observations: strands provide a microscopic model of space, black hole horizons and gravitons, explain mass, particles and black hole radiation, imply general relativity without modifications, prevent singularities and wormholes, reproduce cosmology (see step 6), but predict the lack of elementary dark matter particles. Strands are also complete: no question of quantum gravity is unanswered.
Any complete description of nature has to be strange. To satisfy this requirement for gravitation, the following animation, made by Jason Hise, shows how black hole rotation is modelled in the strand tangle model. (The flattening of the horizon at the poles is not shown.) With a bit of imagination, you can determine the location of the ergosphere.
Step 4. The strand tangle model about wave functions and field theory
Pedagogical. For physicists, the best introduction to the strand tangle model is the preprint showing how wave functions, quantum theory, fermions and bosons, the three gauge interactions, the three elementary particle generations and unique elementary particle masses follow from strands. A longer introduction is found on this page.
Wave functions and interactions. A single principle is used to derive the Schrödinger equation, the Pauli equation, and the Dirac equation. Spin 1/2, fermion behaviour, mass, and, above all, the observed elementary particles and the observed gauge interactions are deduced - without any modification.
Complete. The strand tangle model explains why all measurements are electromagnetic, why only massive particles can have electric charge, why the spin-statistics theorem holds, and why the origin of gauge interactions settles the Yang-Mills millennium problem. (The latter topic is also explained here.) In short, it is shown that all "laws" of physics are uniquely defined, without any possible variation or alternative. There is only one possible universe.
From 9 lines to 1 line. In 2022, the strand tangle model, with its one line, explains about 8.2 lines of the 9 lines that describe all of physics and of nature. The strand tangle model also agrees with all experiments. The remaining constants of line 9 still have to be deduced. The task is not finished. But: no other theory in the literature has achieved this much. (In fact, two other approaches have similar results. The octonion model by Singh, arxiv.org/pdf/2206.06911.pdf, and Connes' non-commutative geometry, arxiv.org/pdf/1004.0464.pdf, both explain more than 8 lines, but both appear to predict additional unobserved particles. A more detailed evaluation is found here.)
Using strands, nature is summarized in just 1 line: General relativity and the standard model, with massive neutrinos, are due to fluctuating strands of Planck radius, for which each crossing switch yields a quantum of action.
Qubits. The strand tangle model also shows how to give concrete meaning to Zizzi’s expression “it from qubit”: qubits can be modelled with strands. So can entanglement and decoherence. And gravity.
Lepton tangles. An animation of the spinning electron tangle can be seen here: https://www.desmos.com/3d/ck2jidmtbd
Use your mouse to play with the 3d visualizations of the three simplest tangles (derived in the various papers) for the electron neutrino, the muon neutrino, and the tau neutrino:
and the simplest tangles for the electron, the
muon and the tau:
All these beautiful 3d visualizations were realized with Blender by Aleksandr, by Lucas and by Mitchell.
Step 5: The strand tangle model for the standard model of particle physics
Beautiful. When we look at the starry sky, we admire the vast space, the coloured twinkling stars, and the deep blackness. The strand tangle model proposes an explanation for their origin, their properties and their motion. The foundations of what we find around us – particles, space, horizons and colours of everything we see – are explained.
C. Schiller, A conjecture on deducing general
relativity and the standard model with its fundamental constants from
rational tangles of strands, Physics of Particles and Nuclei
50 (2019) 259–299. Download the published paper at
dx.doi.org/10.1134/S1063779619030055. Read the published paper online for free at
rdcu.be/cdCK7. Download the preprint here, with films.
![]()
Testable. The paper argues that modern physics arises, directly and inevitably, from the Planck scale. Below, the more pedagogical papers and preprints deduce additional experimental predictions and tests. A detailed list of experimental tests is found on the bet page, by clicking here.
Simple. The strand tangle model starts with deducing Dirac’s equation from Dirac’s trick for tangles. Then, tangle classification yields the particle spectrum. Tangle deformations yield, via the Reidemeister moves, the particle gauge interactions groups U(1), SU(3) and broken SU(2). Working out the details gives usual particle physics, with no additions, modifications, or omissions. More details are on this page.
A compact introduction for physicists and physics students is
![]() C. Schiller, On the relation between the three
Reidemeister moves and the three gauge groups, preprint on Researchgate
at https://www.researchgate.net/publication/369794894.
C. Schiller, On the relation between the three
Reidemeister moves and the three gauge groups, preprint on Researchgate
at https://www.researchgate.net/publication/369794894.
C. Schiller, Testing a conjecture on the origin of the
standard model, European Physical Journal Plus 136 (2021)
79. Download it at doi.org/10.1140/epjp/s13360-020-01046-8. Read the published paper online for free at
rdcu.be/cdwSI. Download the
preprint here. ![]()
Elegant. It is regularly claimed that the standard model with massive neutrinos is complex, incomplete, or ugly. The strand tangle model argues the opposite: all particle physics is due to tangled strands fluctuating at the Planck scale. A single fundamental process appears to explain the principle of least action, the Dirac equation, the observed interaction spectrum, the observed gauge symmetry groups, the observed elementary particle spectrum, and the fundamental constants (masses, mixing angles, and coupling constants) describing them. The Lagrangian of the standard model arises, including massive neutrinos, without modifications. Over 100 additional tests and predictions about particle physics beyond the standard model, with massive neutrinos, are deduced. They agree with all experiments. So far, no other approach in the research literature appears to make (almost) any of these predictions. Indeed, it appears that the explanation of the standard model using tangled strands is consistent, complete, correct, hard to vary, and unique. Above all, it is beautifully simple.
A list of experimental predictions is also found here. Parity violation is illustrated in the videos on the topic.
Step 6: Quantum electrodynamics deduced from strands
C. Schiller, Testing a conjecture on quantum
electrodynamics,
Journal of
Geometry and Physics 178 (2022) 104551.
Download the preprint
here. ![]()
Colours and beauty. Strands show how tangles leads to quantum electrodynamics, including electricity, magnetism and optics. Over 40 tests for the conjecture are given. So far, they are all positive. In particular, the strand tangle model appears to allow approaching two old challenges: how to calculate the fine structure constant and how to calculate the lepton masses – both from first principles. The preprint uses the tangle model of particles to deduce estimates. The fine structure constant with its measured value 1/137.036(1) and the lepton masses, in particular the electron mass, are the ingredients that determine all colours, tastes, smells, sounds and most shapes around us. In other words: it is argued that tangles of strands generate all beauty in nature.
Presently, tangles lead to a crude estimate of the fine structure
constant that is correct within 30%. This is not good; but so far,
it is one of just two attempts worldwide to explain the value, ab initio,
using a unified description of particle physics and general relativity.
The spin of leptons.
Leptons consist of three strands. The animation by Jason Hise gives
an impression about how they spin:
The central cube contains the core defining the lepton tangle.
The spinning electron tangle.
Fabrice Neyret, inspired by Jason Hise, produced two animations
showing two options for the spinning electron. Use your mouse to change
point of view:
(alternatively, click here.)
(alternatively, click here.)
The radius of the strands is the Planck length.
The green bar is only added for better visualization; it shows
the orientation of the electron. The tangle tethers reproduce spin 1/2
and fermion behaviour under particle exchange.
The wave function arises from the blurring of the tangle crossings. The tangle
details determine electric charge (every chiral crossing produces an
electric charge e/3), parities (behaviour under mirror reflection and
rotation reversal), lepton number (results from the 3 strands), mass (not
visible directly, via the average rotation speed), electromagnetic
coupling and the fine structure constant (through the statistics of tangle
shapes), and the behaviour in particle reactions (due to the topology of
the rational 3d tangle).
Positrons are mirror tangles rotating in the opposite sense.
More details are found in the published paper on
quantum electrodynamics linked a few paragraphs higher up, and also in the pdf found at step 4.
No other model of the electron achieves all these explanations.
Here is the photon, showing its rotating phase:
(alternatively, click here.)
Step 7: Quantum chromodynamics deduced from strands
Quarks and nuclei. The strand tangle model shows how the tangle model leads to the strong interaction, the quark model, gluon flux tubes, confinement and asymptotic freedom. The existence (new in 2022) of glueballs is predicted. Many other tests for the tangle model are deduced, including the lack of new generations, the lack of CP violation and the lack of deviations from QCD. All consequences agree with the data. In particular, the strand tangle model allows estimating the strong coupling constant and the quark masses ab initio.
The spinning motion of the simplest tangle of
the down quark. Jason Hise also produced the animation for this
case:

Indeed, the tangle model is peculiar – to say the least.
Step 8: Cosmology deduced from strands
![]() C. Schiller, Testing a conjecture on
cosmology and dark energy (preprint).
C. Schiller, Testing a conjecture on
cosmology and dark energy (preprint).
The universe. This and a subsequent preprint on cosmology complete the topic of gravitation. In the strand tangle model, the universe consists of a single closed strand that forms the cosmological horizon and also the particles and the space inside it. Over time, this strand gets more and more tangled. (As one reader said: the universe plays cat's cradle.) This description reproduces usual cosmology and leads to numerous tests and predictions: the universe expands; nothing – no matter, no radiation and no space – exists beyond the cosmological horizon; inflation did not occur; there are no cosmic strings and no higher dimensions; there is no non-trivial topology; there is no bouncing universe; there is just one universe; the luminosity of the universe is always limited by c5/4G; dark matter is not made of unknown elementary particles; if dark matter exists at all, it is made of known matter or black holes or both; dark energy, or vacuum energy, does exist and is a natural consequence of strands; the density of vacuum energy, the cosmological constant, is small; baryogenesis appears to be due to non-perturbative effects.
The strand description of cosmology is promising. However, calculating
the vacuum energy density remains a challenge.
Therefore, clarifying the relation of strands to modified gravity and to the baryonic
Tully-Fisher relation remains a challenge as well.
Outreach
Blog. The blog on research about fundamental physics and strand tangles and the older blogs tell more about general ideas, past mistakes, objections, encountered difficulties, and progress.
*
T-shirt. An important motivation for strand research has always been to support the ailing physics T-shirt industry. For decades, it has been desperate for new designs. Now they are available.
*
History. The strand tangle model is a side result of the free Motion Mountain Physics Textbook series, in particular of Dirac's spin 1/2 demonstration, of the principle of maximum force, of the strand explanation of back hole entropy, and of the meditation time offered by the Munich subway. Strands reduce the 9 lines describing textbook physics to a single principle (that fits on a T-shirt), and make clear predictions for experiments and calculations. If you want to bet about the outcomes, to evaluate your chances, to comment, or if you want to help with animations similar to these, write to christoph@motionmountain.net.
*
Technicalities. The strand tangle model reproduces the Lagrangians of the standard model and general relativity, explains neutrino masses without a see-saw mechanism, explains the number of generations and the particle spectrum, deduces all Feynman diagrams and propagators, explains the gauge groups U(1), SU(2) and SU(3), explains the fundamental constants ab initio, solves the hierarchy problem, solves the strong CP problem, predicts the validity of particle physics and of general relativity up to the Planck scale without any intermediate energy scale, implies that the weak interaction violates parity maximally, explains the equality of proton and positron charge, has no problems with anomalies, predicts no issues with baryogenesis, has no grand unification, has no supersymmetry, has no additional spatial dimensions, has no inflation, no inflaton and no dilaton, solves black hole and singularity issues, implies gravitational waves, has no dark matter particles, has a naturally small cosmological constant, solves various problems with gauge theories, answers Hilbert's sixth problem, and explains the principle of least action.
Acknowledgements
Several of these articles - see them all here - were supported by grants from Klaus Tschira via his Klaus Tschira Foundation: Eur Phys J Plus, Indian J Phys, J Geom Phys, IJGMMP, Z f Naturf, dark energy preprint, emergent quantum theory preprint, first Bronshtein cube preprint.
Volume VI of Motion Mountain
Older work. A more extensive, more passionate, but also older and less precise presentation is the original text on the strand model. It was written as a research volume and continues the adventure of the five textbook volumes.
Strands in other languages
A 'strand' is best translated in Dutch as draad, in French as fil, in German as Faden, in Italian as filo and in Spanish as hilo. The mathematical concept of 'tangle' is best translated in Dutch as wirwar, in French as enchevêtrement, in German as Gewirr, in Italian as groviglio and in Spanish as enredo. A 'tether' is best translated in Dutch as lijn, in French as lien, in German as Leine, in Italian as nesso and in Spanish, for example, as vínculo.
Publication list
On the Planck limits as foundations of the strand tangle model
C. Schiller, Tests for maximum force and maximum power, Physical Review D 104 (2021) 124079.
C. Schiller, Comment on "Maximum force and cosmic censorship", Physical Review D 104 (2021) 068501.
Older papers on the topic can be found via Google Scholar and via ResearchGate.
On deducing general relativity from strand tangles
On deducing the standard model with massive neutrinos from strand tangles
Research preprints linked here.
* *